
【题目】(1)已知:点(x,y)在直线y=﹣x+1上,且x2+y2=2,求x7+y7的值.
(2)计算:
![]()
(3)已知a、b、c是直角三角形△ABC的角A、B、C所对的边,∠C=90°.求:![]() 的值.
的值.
【答案】(1)![]() ;(2)0; (3)0
;(2)0; (3)0
【解析】
(1)根据点(x,y)在直线y=-x+1上,得出x+y=1,进而求出xy的值,再利用因式分解法求出x7+y7的值;
(2)首先设![]() =z,再替换后整理得出即可;
=z,再替换后整理得出即可;
(3)将原式分组进行计算,再利用三角形三边关系求出即可.
解:(1)∵x2+y2=21=(x+y)2=x2+y2+2xy=2+2xyxy=![]() ,
,
∴x3+y3=(x+y)33xy(x+y)=13×(![]() )=
)=![]() x4+y4=(x2+y2)22x2y2=42(
x4+y4=(x2+y2)22x2y2=42(![]() )2=
)2=![]() ,
,
∴x7+y7=(x3+y3)(x4+y4)x3y3(x+y)=![]() ×
×![]() (
(![]() )3×1=
)3×1=![]() ;
;
(2)设![]() =z,
=z,
则原式=![]() =0;
=0;
(3)原式=![]()
=![]()
=![]()
=0.


科目:初中数学 来源: 题型:
【题目】如图所示,⊙O的半径为4,点A是⊙O上一点,直线l过点A;P是⊙O上的一个动点(不与点A重合),过点P作PB⊥l于点B,交⊙O于点E,直径PD延长线交直线l于点F,点A是![]() 的中点.
的中点.
(1)求证:直线l是⊙O的切线;
(2)若PA=6,求PB的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,直线
中,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() 抛物线
抛物线![]() 的对称轴是直线
的对称轴是直线![]() 与
与![]() 轴的交点为点
轴的交点为点![]() 且经过点
且经过点![]() 两点.
两点.
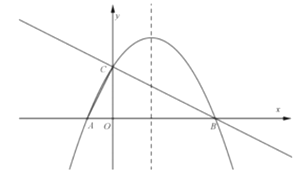
(1)求抛物线的解析式;
(2)点![]() 为抛物线对称轴上一动点,当
为抛物线对称轴上一动点,当![]() 的值最小时,请你求出点
的值最小时,请你求出点![]() 的坐标;
的坐标;
(3)抛物线上是否存在点![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() 使得以点
使得以点![]() 为顶点的三角形与
为顶点的三角形与![]() 相似?若存在,请直接写出点
相似?若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自2016年共享单车上市以来,给人们的出行提供了便利,受到了广大市民的青睐,某公司为了了解员工上下班回家的路程(设路程为x千米)情况,随机抽取了若干名员工进行了问卷调查,现将这些员工的调查结果分为四个等级,A:0≤x≤3;B:3<x≤6;C:6<x≤9;D:x>9;并将调查结果绘制成如下两幅不完整的统计图:
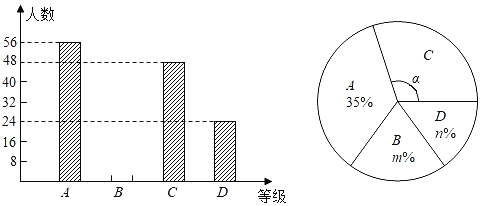
(1)请补全上面的条形统计图,并求m和n的值;
(2)在扇形统计图中,求扇形“C”所对应的圆心角α的度数;
(3)若该公司有600名员工,请你估计该公司路程在6千米以上选择共享单车上下班的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E、F分别是平行四边形ABCD的边AD、BC上的点,且BE∥DF,AC分别交BE、DF于点G、H.下列结论:①四边形BFDE是平行四边形;②△AGE≌△CHF;③BG=DH;④S△AGE:S△CDH=GE:DH,其中正确的个数是( )
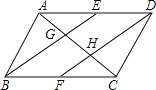
A.1B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)图象如图,下列结论:①abc>0;②2a+b=0;③当m≠1时,a+b>am2+bm;④a-b+c>0;⑤若ax12+bx1=ax22+bx2,且x1≠x2,x1+x2=2.其中正确的有( )
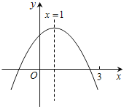
A.②④B.②⑤C.①②③D.②③⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业设计了一款工艺品,每件的成本是50元,为了合理定价,投放市场进行试销.据市场调查,销售单价是100元时,每天的销售量是50件,而销售单价每降低1元,每天就可多售出5件,但要求销售单价不得低于成本.
(1)当销售单价为70元时,每天的销售利润是多少?
(2)求出每天的销售利润y(元)与销售单价x(元)之间的函数关系式,并求出自变量![]() 的取值范围;
的取值范围;
(3)如果该企业每天的总成本不超过7000元,那么销售单价为多少元时,每天的销售利润最大?最大利润是多少?(每天的总成本=每件的成本×每天的销售量)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司生产的某种时令商品每件成本为20元,经过市场调研发现,这种商品在未来40天内的日销售量![]() 件
件![]() 与时间
与时间![]() 天
天![]() 的关系如下表:
的关系如下表:
时间 | 1 | 3 | 5 | 10 | 36 |
|
日销售量 | 94 | 90 | 86 | 76 | 24 |
|
已知未来40天内,前20天该商品每天的价格![]() 元
元![]() 件
件![]() 与时间t的函数关系式为
与时间t的函数关系式为![]() (
(![]() ,且t为整数),后20天该商品每天的价格
,且t为整数),后20天该商品每天的价格![]() 元
元![]() 件
件![]() 与时间t的函数关系式为
与时间t的函数关系式为![]() (
(![]() ,且t为整数).
,且t为整数).
![]() 求m与t之间的函数关系式;
求m与t之间的函数关系式;
![]() 未来40天内,后20天中哪一天的日销售利润最大
未来40天内,后20天中哪一天的日销售利润最大![]() 最大日销售利润是多少.
最大日销售利润是多少.
![]() 在实际销售的前20天中,该公司决定每销售一件商品,就捐赠
在实际销售的前20天中,该公司决定每销售一件商品,就捐赠![]() 元给希望工程
元给希望工程![]() 公司查阅销售记录发现,前20天中,扣除捐赠后的日销售利润随时间t的增大而增大,求a的取值范围.
公司查阅销售记录发现,前20天中,扣除捐赠后的日销售利润随时间t的增大而增大,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com