
【题目】某企业设计了一款工艺品,每件的成本是50元,为了合理定价,投放市场进行试销.据市场调查,销售单价是100元时,每天的销售量是50件,而销售单价每降低1元,每天就可多售出5件,但要求销售单价不得低于成本.
(1)当销售单价为70元时,每天的销售利润是多少?
(2)求出每天的销售利润y(元)与销售单价x(元)之间的函数关系式,并求出自变量![]() 的取值范围;
的取值范围;
(3)如果该企业每天的总成本不超过7000元,那么销售单价为多少元时,每天的销售利润最大?最大利润是多少?(每天的总成本=每件的成本×每天的销售量)
【答案】(1)4000;(2)y=-5![]() (50≤x≤100);(3)销售单价为82元时,每天的销售利润最大,最大利润为4480元.
(50≤x≤100);(3)销售单价为82元时,每天的销售利润最大,最大利润为4480元.
【解析】
试题分析:(1)根据“利润=(售价-成本)×销售量”即可求解;(2))根据“利润=(售价-成本)×销售量”即可求得函数关系式,根据售价不小于50元即可确定x的取值范围;(3)先由“每天的总成本不超过7000元”列出关于x的不等式50(-5x+550)≤7000,通过解不等式来求x的取值范围,再把(2)中的二次函数解析式转化为顶点式方程,利用二次函数图象的性质进行解答即可.
试题解析:解:(1)当销售单价为70元时,每天的销售利润是:
[50+(100-70)]×(70-50)=4000(元)
(2)由题得 y=[50+5(100-x)](x-50)
=-5![]()
由x≥50,100-x≥50得50≤x≤100
![]() y=-5
y=-5![]() (50≤x≤100)
(50≤x≤100)
(3)∵该企业每天的总成本不超过7000元
∴50[50+5(100-x)]≤7000
解得x≥82
由(2)可知50≤x≤100
∴82≤x≤100
∵抛物线y=-5![]() 的对称轴为x=80且a=-5<0
的对称轴为x=80且a=-5<0
∴抛物线开口向下,在对称轴右侧,y随x增大而减小.
∴当x=82时,y最大=4480,
即 销售单价为82元时,每天的销售利润最大,最大利润为4480元.


科目:初中数学 来源: 题型:
【题目】某商店销售A,B两种商品,每件A商品的售价比B商品少10元.购买5件A商品比购买3件B商品多10元.设每件A商品的售价为x元.
(1)每件B商品的售价为______元(用含x的式子表示);
(2)求A,B商品每件的售价各多少元?
(3)元旦期间,该商店决定对A,B两种商品进行促销活动,具体办法是:
方案一:购买A商品超出15件后,超出部分五折销售,不超出部分不享受任何折扣;B商品无论多少一律九折.
方案二:无论买多少,A,B商品一律八折.
若小红打算到该商店购买m件A商品和20件B商品,选择哪种方案购买更实惠(两种优惠方案不能同时享受)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装专卖店老板对第一季度男、女服装的销售收入进行统计,并绘制了扇形统计图(如图)。由于三月份展开促销活动,男女服装的销售收入分别比二月份增长了40%,64%,已知第一季度男女服装的销售总收入为20万元。

(1)二月份销售收入为_______万元。三月份销售收入为______万元。
(2)二月份男女服装的销售收入分别是多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,∠B=90°,AB=BC,BD=CE,M是AC边上的中点。
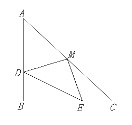
(1)求证:△DEM是等腰直角三角形.
(2)已知AD=4,CE=3,求DE的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分9分)某百货大搂服装柜在销售中发现:“七彩”牌童装平均每天可售出20件,每件盈利40元.为了迎接“元旦”,商场决定采取适当的降价措施,扩大销售量,增加盈利,减少库存.经市场调查发现:如果每件童装降价1元,那么平均每天就可多售出2件.
(1)要想平均每天销售这种童装盈利1200元,那么每件童装应降价多少元?
(2)用配方法说明:要想盈利最多,每件童装应降价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是边长为4cm的等边三角形,AD为BC边上的高,点P沿BC向终点C运动,速度为1cm/s,点Q沿CA、AB向终点B运动,速度为2cm/s,若点P、Q两点同时出发,设它们的运动时间为x(s).
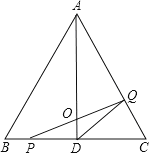
(l)求x为何值时,PQ⊥AC;x为何值时,PQ⊥AB?
(2)当O<x<2时,AD是否能平分△PQD的面积?若能,说出理由;
(3)探索以PQ为直径的圆与AC的位置关系,请写出相应位置关系的x的取值范围(不要求写出过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品的进价为每件40元.当售价为每件60元时,每星期可卖出300件,现需降价处理,且经市场调查:每降价1元,每星期可多卖出20件.在确保盈利的前提下,解答下列问题:
(1)若设每件降价x元、每星期售出商品的利润为y元,请写出y与x的函数关系式,并求出自变量x的取值范围;
(2)若降价的最小单位为1元,则当降价多少元时,每星期的利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AB是⊙O的直径,点P在BA的延长线上,PD切⊙O于点C,BD⊥PD,垂足为D,连接BC。
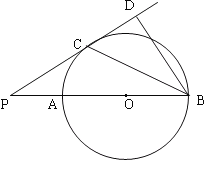
求证:(1)BC平分∠PBD;
(2)BC2=AB·BD。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com