
【题目】已知:如图,AB是⊙O的直径,点P在BA的延长线上,PD切⊙O于点C,BD⊥PD,垂足为D,连接BC。
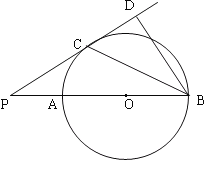
求证:(1)BC平分∠PBD;
(2)BC2=AB·BD。
【答案】见解析
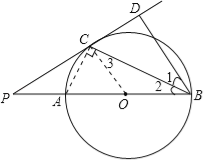
【解析】试题分析:(1)连接OC.可发现∠OCB和∠DBC同为∠DCB的余角,而∠OCB=∠OBC,由此可得∠OBC=∠DBC,即BC平分∠PBD;
(2)连接AC.证明△ABC∽△CBD即可.
【解答】证明:(1)连接OC.(1分)
∵PD切⊙O于点C,
又∵BD⊥PD,
∴OC∥BD.
∴∠1=∠3.(2分)
又∵OC=OB,
∴∠2=∠3.(3分)
∴∠1=∠2,即BC平分∠PBD.(4分)
(2)连接AC.
∵AB是⊙O的直径,
∴∠ACB=90°.(5分)
又∵BD⊥PD,
∴∠ACB=∠CDB=90°(6分)
又∵∠1=∠2,
∴△ABC∽△CBD;(7分)
∴![]() ,∴BC2=ABBD.(8分)
,∴BC2=ABBD.(8分)


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案科目:初中数学 来源: 题型:
【题目】某企业设计了一款工艺品,每件的成本是50元,为了合理定价,投放市场进行试销.据市场调查,销售单价是100元时,每天的销售量是50件,而销售单价每降低1元,每天就可多售出5件,但要求销售单价不得低于成本.
(1)当销售单价为70元时,每天的销售利润是多少?
(2)求出每天的销售利润y(元)与销售单价x(元)之间的函数关系式,并求出自变量![]() 的取值范围;
的取值范围;
(3)如果该企业每天的总成本不超过7000元,那么销售单价为多少元时,每天的销售利润最大?最大利润是多少?(每天的总成本=每件的成本×每天的销售量)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,从一个半径为1的圆形铁皮中剪下一个圆心角为90°的扇形BAC.
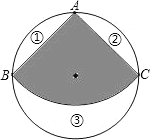
(1)求这个扇形的面积;
(2)若将扇形BAC围成一个圆锥的侧面,这个圆锥的底面直径是多少?能否从最大的余料③中剪出一个圆做该圆锥的底面?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文艺团体为“希望工程”募捐组织了一场义演,共售出1000张票,筹出票款6920元,且每张成人票8元,学生票5元.
(1)问成人票与学生票各售出多少张?
(2)若票价不变,仍售出1000张票,所得的票款可能是7290元吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了响应政府提出的由中国制造向中国创造转型的号召,某公司自主设计了一款成本为40元的可控温杯,并投放市场进行试销售,经过调查发现该产品每天的销售量y(件)与销售单价x(元)满足一次函数关系:y=﹣10x+1200.
(1)求利润S(元)与销售单价x(元)之间的关系式;
(2)当销售单价定为多少时,该公司每天获取的利润最大?最大利润是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com