
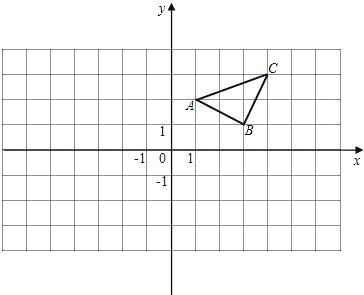
【题目】(1)画出△ABC关于y轴的对称图形![]() ,并写出
,并写出![]() 的顶点坐标;
的顶点坐标;
(2)在x轴上求作点P,使PA+PC的值最小.
【答案】(1)作图见解析;A′(-1,2),B′(-3,1),C′(-4,3)(2) 作图见解析。
【解析】
试题分析:(1)根据轴对称的性质分别作出A、B、C三点关于y轴的对称点A′、B′、C′,分别连接各点即可;
(2)先找出C先找出C点关于x轴对称的点C″(4,-3),连接C″A交x轴于点P,则点p即为所求点.
试题解析:(1)
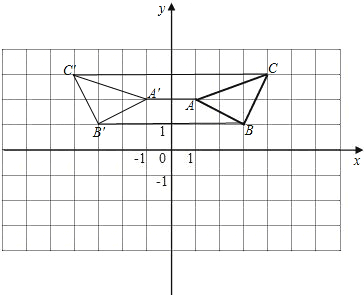
分别作A、B、C的对称点,A′、B′、C′,由三点的位置可知:
A′(-1,2),B′(-3,1),C′(-4,3)
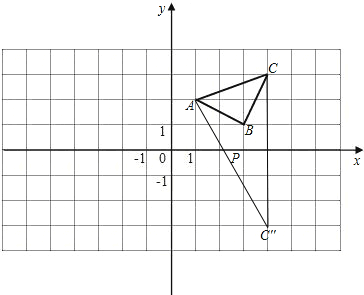
(2)先找出C点关于x轴对称的点C″(4,-3),连接C″A交x轴于点P,
(或找出A点关于x轴对称的点A″(1,-2),连接A″C交x轴于点P)则P点即为所求点.


科目:初中数学 来源: 题型:
【题目】对式子“0.5x”可以赋予含义为:一支圆珠笔的笔芯价格为0.5元,若买x支笔芯,则共付款0.5x元.请你对方程“0.5(x﹣1)=8”赋予一个含义_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场购进一种单价为![]() 元的篮球,如果以单价
元的篮球,如果以单价![]() 元售出,那么每天可售出50个.根据销售经验,售价每提高
元售出,那么每天可售出50个.根据销售经验,售价每提高![]() 元.销售量相应减少1个。
元.销售量相应减少1个。
(1)假设销售单价提高![]() 元,那么销售每个篮球所获得的利润是_____元;这种篮球每天的销售量是_________个。
元,那么销售每个篮球所获得的利润是_____元;这种篮球每天的销售量是_________个。
(2)假设每天销售这种篮球所得利润为y ,请用含![]() 的代数式表示y。
的代数式表示y。
(3)假如你是商场老板,为了在出售这种篮球时获得最大利润,你该提高多少元?最大利润是多少?请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校政教处倡导“光盘行动”,让同学们珍惜粮食,但发现还是有少数同学们就餐时剩余饭菜较多,为了让同学们理解这次活动的重要性,政教处在某天午餐中,分别按照七、八、九三个年级总人数的同样比例随机调查了三个年级部分同学这餐饭菜的剩余情况,分为三类:A(没有剩余)、B(有少量剩余)、C(剩余一半及以上),并将结果统计后绘制成了如图所示的不完整的统计图.
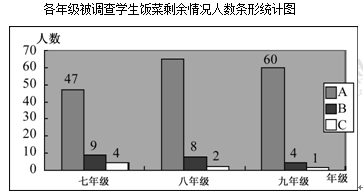
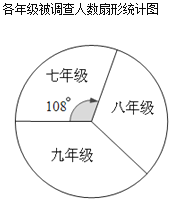
(1)这次被调查的同学共有名;
(2)八年级被调查的学生共有名;
(3)通过数据分析,估计这次被调查的所有学生一餐浪费的食物可以供8人用一餐.据此估算,该校1000名学生这餐饭菜没有浪费的学生有多少人?这餐浪费的食物可供多少人食用一餐?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业设计了一款工艺品,每件的成本是50元,为了合理定价,投放市场进行试销.据市场调查,销售单价是100元时,每天的销售量是50件,而销售单价每降低1元,每天就可多售出5件,但要求销售单价不得低于成本.
(1)当销售单价为70元时,每天的销售利润是多少?
(2)求出每天的销售利润y(元)与销售单价x(元)之间的函数关系式,并求出自变量![]() 的取值范围;
的取值范围;
(3)如果该企业每天的总成本不超过7000元,那么销售单价为多少元时,每天的销售利润最大?最大利润是多少?(每天的总成本=每件的成本×每天的销售量)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】本市出租车的收费标准为:3千米以内(含3千米)收费5元,超过3千米的部分每千米收费1.20元(不足1千米按1千米计算),另加收0.60元的返空费.
(1)设行驶路程为x千米(![]() ≥3且取整数),用x表示出应收费y元的代数式;
≥3且取整数),用x表示出应收费y元的代数式;
(2)当收费为10.40元时,该车行驶路程不超过多少千米?路程数在哪个范围内?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D。AF平分∠CAB,交CD于点E,交CB于点F。
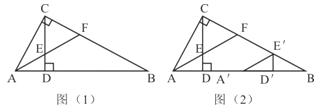
(1)求证:CE=CF。
(2)将图(1)中的△ADE沿AB向右平移到△A′D′E′的位置,使点E′落在BC边上,其它条件不变,如图(2)所示。试猜想:BE′与CF有怎样的数量关系?请证明你的结论。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆货车从百货大楼出发负责送货,向东走了4千米到达小明家,继续向东走了1.5千米到达小红家,然后向西走了8.5千米到达小刚家,最后返回百货大楼.
(1)以百货大楼为原点,向东为正方向,1个单位长度表示1千米,请你在数轴上标出小明、小红、小刚家的位置.(小明家用点A表示,小红家用点B表示,小刚家用点C表示)
![]()
(2)小明家与小刚家相距多远?
(3)若货车每千米耗油1.5升,那么这辆货车此次送货共耗油多少升?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com