
【题目】如图,四边形ABCD的∠BAD=∠C=90°,AB=AD,AE⊥BC于E,△BEA旋转一定角度后能与△DFA重合.
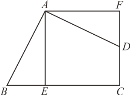
(1)旋转中心是哪一点?
(2)旋转了多少度?
(3)若AE=5cm,求四边形ABCD的面积.
【答案】(1)点A为旋转中心;(2)旋转了90°或270°;(3)四边形ABCD的面积为25cm2.
【解析】
(1)根据图形确定旋转中心即可;
(2)对应边AE、AF的夹角即为旋转角,再根据正方形的每一个角都是直角解答;
(3)根据旋转变换只改变图形的位置不改变图形的形状与大小可得△BAE的面积等于△DAF的面积,从而得到四边形ABCD的面积等于正方形AECF的面积,然后求解即可.
(1)由图可知,点A为旋转中心;
(2)在四边形ABCD中,∠BAD=90°,所以,旋转了90°或270°;
(3)由旋转性质知,AE=AF,∠F=∠AEB=∠AEC=∠C=90°
∴四边形AECF是正方形,
∵△BEA旋转后能与△DFA重合,
∴△BEA≌△DFA,
∴S△BEA=S△DFA,
∴四边形ABCD的面积=正方形AECF的面积,
∵AE=5cm,
∴四边形ABCD的面积=52=25cm2.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,直线
中,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() 抛物线
抛物线![]() 的对称轴是直线
的对称轴是直线![]() 与
与![]() 轴的交点为点
轴的交点为点![]() 且经过点
且经过点![]() 两点.
两点.
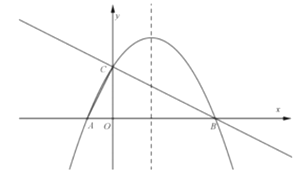
(1)求抛物线的解析式;
(2)点![]() 为抛物线对称轴上一动点,当
为抛物线对称轴上一动点,当![]() 的值最小时,请你求出点
的值最小时,请你求出点![]() 的坐标;
的坐标;
(3)抛物线上是否存在点![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() 使得以点
使得以点![]() 为顶点的三角形与
为顶点的三角形与![]() 相似?若存在,请直接写出点
相似?若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业设计了一款工艺品,每件的成本是50元,为了合理定价,投放市场进行试销.据市场调查,销售单价是100元时,每天的销售量是50件,而销售单价每降低1元,每天就可多售出5件,但要求销售单价不得低于成本.
(1)当销售单价为70元时,每天的销售利润是多少?
(2)求出每天的销售利润y(元)与销售单价x(元)之间的函数关系式,并求出自变量![]() 的取值范围;
的取值范围;
(3)如果该企业每天的总成本不超过7000元,那么销售单价为多少元时,每天的销售利润最大?最大利润是多少?(每天的总成本=每件的成本×每天的销售量)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学学习小组根据函数学习的经验,对一个新函数![]() 的图象和性质进行了如下探究:
的图象和性质进行了如下探究:
![]() 列表,下表是函数
列表,下表是函数![]() 与自变量
与自变量![]() 的几组对应值
的几组对应值
| ··· |
|
|
|
|
|
|
|
|
|
| ··· |
| ··· |
|
|
|
|
|
|
|
|
|
| ··· |
请直接写出![]()
![]()
![]()
![]() 如图,在平面直角系
如图,在平面直角系![]() 中,描出上表中各对对应值为坐标的点 (其中
中,描出上表中各对对应值为坐标的点 (其中![]() 为横坐标,
为横坐标,![]() 为纵坐标),并根据描出的点画出函数的图象
为纵坐标),并根据描出的点画出函数的图象
![]() 观察所画出的函数图象,写出该函数的性质(写一条性质即可)
观察所画出的函数图象,写出该函数的性质(写一条性质即可)
![]() 请结合画出的函数图象与表格中数据,直接写出关于
请结合画出的函数图象与表格中数据,直接写出关于![]() 的不等式的解集:
的不等式的解集:![]()
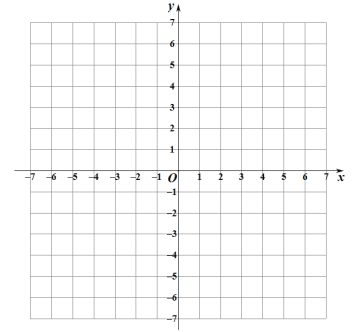
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于A、B两点,与
轴交于A、B两点,与![]() 轴交于点C,抛物线的对称轴交
轴交于点C,抛物线的对称轴交![]() 轴于点D,已知点A的坐标为(-1,0),点C的坐标为(0,2).
轴于点D,已知点A的坐标为(-1,0),点C的坐标为(0,2).
(1)求抛物线的解析式;
(2)在抛物线的对称轴上是否存在点P,使△PCD是以CD为腰的等腰三角形?如果存在,请直接写出点P的坐标;如果不存在,请说明理由.
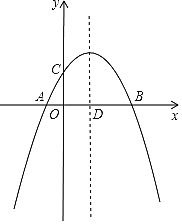
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,CD是△ABC的中线,如果![]() 上的所有点都在△ABC的内部或边上,则称
上的所有点都在△ABC的内部或边上,则称![]() 为△ABC的中线弧.
为△ABC的中线弧.
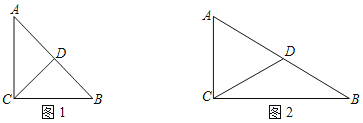
(1)在Rt△ABC中,∠ACB=90°,AC=1,D是AB的中点.
①如图1,若∠A=45°,画出△ABC的一条中线弧![]() ,直接写出△ABC的中线弧
,直接写出△ABC的中线弧![]() 所在圆的半径r的最小值;
所在圆的半径r的最小值;
②如图2,若∠A=60°,求出△ABC的最长的中线弧![]() 的弧长l.
的弧长l.
(2)在平面直角坐标系中,已知点A(2,2),B(4,0),C(0,0),在△ABC中,D是AB的中点.求△ABC的中线弧![]() 所在圆的圆心P的纵坐标t的取值范围.
所在圆的圆心P的纵坐标t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司生产的某种时令商品每件成本为20元,经过市场调研发现,这种商品在未来40天内的日销售量![]() 件
件![]() 与时间
与时间![]() 天
天![]() 的关系如下表:
的关系如下表:
时间 | 1 | 3 | 5 | 10 | 36 |
|
日销售量 | 94 | 90 | 86 | 76 | 24 |
|
已知未来40天内,前20天该商品每天的价格![]() 元
元![]() 件
件![]() 与时间t的函数关系式为
与时间t的函数关系式为![]() (
(![]() ,且t为整数),后20天该商品每天的价格
,且t为整数),后20天该商品每天的价格![]() 元
元![]() 件
件![]() 与时间t的函数关系式为
与时间t的函数关系式为![]() (
(![]() ,且t为整数).
,且t为整数).
![]() 求m与t之间的函数关系式;
求m与t之间的函数关系式;
![]() 未来40天内,后20天中哪一天的日销售利润最大
未来40天内,后20天中哪一天的日销售利润最大![]() 最大日销售利润是多少.
最大日销售利润是多少.
![]() 在实际销售的前20天中,该公司决定每销售一件商品,就捐赠
在实际销售的前20天中,该公司决定每销售一件商品,就捐赠![]() 元给希望工程
元给希望工程![]() 公司查阅销售记录发现,前20天中,扣除捐赠后的日销售利润随时间t的增大而增大,求a的取值范围.
公司查阅销售记录发现,前20天中,扣除捐赠后的日销售利润随时间t的增大而增大,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A是反比例函数y=![]() 图象在第一象限上的一点,连结AO并延长交图象的另一分支于点B,延长BA至点C,过点C作CD⊥x轴,垂足为D,交反比例函数图象于点E.若
图象在第一象限上的一点,连结AO并延长交图象的另一分支于点B,延长BA至点C,过点C作CD⊥x轴,垂足为D,交反比例函数图象于点E.若![]() ,△BDC的面积为6,则k=_____.
,△BDC的面积为6,则k=_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com