
【题目】已知二次函数y=ax2+bx+c的图象如图所示,有以下结论:①abc>0;②a-b+c<0;③2a=b;④4a+2b+c>0;⑤若点(-2,y1)和(-![]() ,y2)在该图象上,则y1>y2. 其中正确的结论个数是 ( )
,y2)在该图象上,则y1>y2. 其中正确的结论个数是 ( )
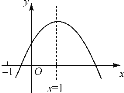
A.1个B.2个C.3个D.4个
 特高级教师点拨系列答案
特高级教师点拨系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,∠EOF=60°,在射线OE上取一点A,使OA=10cm,在射线OF上取一点B,使OB=16cm.以OA、OB为邻边作平行四边形OACB.若点P在射线OF上,点Q在线段CA上,且CQ:OP=1:2.设CQ=a(a>0).

(1)连接PQ,当a=2时,求线段PQ的长度.
(2)若以点P、B、C、Q四点为顶点的四边形是平行四边形时,求a的值.
(3)连接PQ,以PQ所在的直线为对称轴,作点C关于直线PQ的对称点C',当点C′恰好落在平行四边形OACB的边上或者边所在的直线上时,直接写出a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知D、E、F分别是等边△ABC的边AB、BC、AC上的点,且DE⊥BC、EF⊥AC、FD⊥AB,则下列结论不成立的是( )
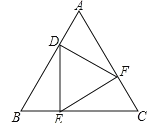
A.△DEF是等边三角形
B.△ADF≌△BED≌△CFE
C.DE=![]() AB
AB
D.S△ABC=3S△DEF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,将一个图形绕原点顺时针方向旋转![]() 称为一次“直角旋转,已知
称为一次“直角旋转,已知![]() 的三个顶点的坐标分别为
的三个顶点的坐标分别为![]() ,
,![]() ,
,![]() ,完成下列任务:
,完成下列任务:
(1)画出![]() 经过一次直角旋转后得到的
经过一次直角旋转后得到的![]() ;
;
(2)若点![]() 是
是![]() 内部的任意一点,将
内部的任意一点,将![]() 连续做
连续做![]() 次“直角旋转”(
次“直角旋转”(![]() 为正整数),点
为正整数),点![]() 的对应点
的对应点![]() 的坐标为
的坐标为![]() ,则
,则![]() 的最小值为 ;此时,
的最小值为 ;此时,![]() 与
与![]() 的位置关系为 .
的位置关系为 .
(3)求出点![]() 旋转到点
旋转到点![]() 所经过的路径长.
所经过的路径长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】金松科技生态农业养殖有限公司种植和销售一种绿色羊肚菌,已知该羊肚菌的成本是12元/千克,规定销售价格不低于成本,又不高于成本的两倍.经过市场调查发现,某天该羊肚菌的销售量y(千克)与销售价格x(元/千克)的函数关系如下图所示:

(1)求y与x之间的函数解析式;
(2)求这一天销售羊肚菌获得的利润W的最大值;
(3)若该公司按每销售一千克提取1元用于捐资助学,且保证每天的销售利润不低于3600元,问该羊肚菌销售价格该如何确定.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解我县中学生参加“新冠肺炎知识”竞赛成绩的情况,随机抽查了部分参赛学生的成绩,根据成绩分成如下四个组:A:60≤x<70,B:70≤x<80,C:80≤x<90,D:90≤x≤100,并制作出如下的扇形统计图和直方图.请根据图表信息解答下列问题:
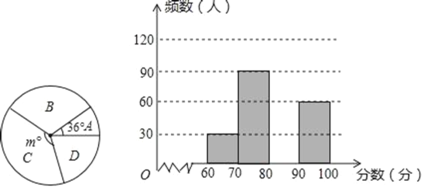
(1)扇形统计图中的m= ,并在图中补全频数分布直方图;
(2)小明的成绩是所有被抽查学生成绩的中位数 ,据此推断他的成绩在 组;
(3)4个小组每组推荐1人,然后从4人中随机抽取2人参加颁奖典礼,恰好抽中A,C两组学生的概率是多少?请列表或画树状图说明;
(4)若我县学生人数为18000人,请根据上述调查结果,估计我县学生成绩在C、D两组的共多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为
为![]() 的中点,动点
的中点,动点![]() 从点
从点![]() 出发沿
出发沿![]() 的方向在
的方向在![]() 和
和![]() 上运动,将矩形沿
上运动,将矩形沿![]() 折叠,点
折叠,点![]() 落在点
落在点![]() 处,当点
处,当点![]() 恰好落在矩形的对角线上时(不与矩形顶点重合),点
恰好落在矩形的对角线上时(不与矩形顶点重合),点![]() 运动的距离为__________.
运动的距离为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂生产的甲、乙两种产品,已知2件甲商品的出厂总价与3件乙商品的出厂总价相同,3件甲商品的出厂总价比2件乙商品的出厂总价多1500元.
(1)求甲、乙商品的出厂单价分别是多少?
(2)某销售商计划购进甲商品200件,购进乙商品的数量是甲的4倍.恰逢该厂正在对甲商品进行降价促销活动,甲商品的出厂单价降低了![]() ,该销售商购进甲的数量比原计划增加了
,该销售商购进甲的数量比原计划增加了![]() ,乙的出厂单价没有改变,该销售商购进乙的数量比原计划少了
,乙的出厂单价没有改变,该销售商购进乙的数量比原计划少了![]() .结果该销售商付出的总货款与原计划的总货款恰好相同,求
.结果该销售商付出的总货款与原计划的总货款恰好相同,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com