
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,正方形
,正方形![]() 的边长为2,将正方形
的边长为2,将正方形![]() 绕点
绕点![]() 旋转一周,连接
旋转一周,连接![]() 、
、![]() 、
、![]() .
.
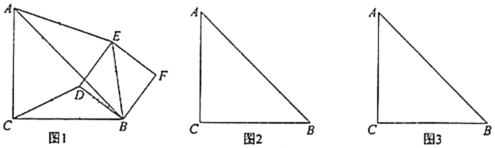
(1)猜想:![]() 的值是__________,直线
的值是__________,直线![]() 与直线
与直线![]() 相交所成的锐角度数是__________;
相交所成的锐角度数是__________;
(2)探究:直线![]() 与
与![]() 垂直时,求线段
垂直时,求线段![]() 的长;
的长;
(3)拓展:取![]() 的中点
的中点![]() ,连接
,连接![]() ,直接写出线段
,直接写出线段![]() 长的取值范围.
长的取值范围.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() 或
或![]() ;(3)(3)
;(3)(3)![]() .
.
【解析】
(1)证明△CBD∽△ABE,相似比为![]() ,△ABE可以看做△CBD绕点B逆时针旋转45°后放大
,△ABE可以看做△CBD绕点B逆时针旋转45°后放大![]() 得到,故直线
得到,故直线![]() 与直线
与直线![]() 相交所成的锐角度数是45°;
相交所成的锐角度数是45°;
(2)证明![]() ,得到
,得到![]() ,分点
,分点![]() 在线段
在线段![]() 上和点
上和点![]() 在线段
在线段![]() 延长线上两类讨论,分别求出AE长,即可求出CD;
延长线上两类讨论,分别求出AE长,即可求出CD;
(3)延长EF到G使得FG=EF,连接AG,BG,则△BFG为等腰直角三角形,求出BG,证明MF=![]() ,根据三角形三边关系求出AG取值范围,问题得解.
,根据三角形三边关系求出AG取值范围,问题得解.
解:(1)由题意得,△ABC, △EBD都是等腰直角三角形,
∴![]() ,
,![]()
∴![]()
∴△CBD∽△ABE
∴![]() ,△ABE可以看做△CBD绕点B逆时针旋转45°后放大
,△ABE可以看做△CBD绕点B逆时针旋转45°后放大![]() 得到,故直线
得到,故直线![]() 与直线
与直线![]() 相交所成的锐角度数是45°;
相交所成的锐角度数是45°;
(2)∵![]() 是腰长为4的等腰直角三角形,四边形
是腰长为4的等腰直角三角形,四边形![]() 的边长为2的正方形,
的边长为2的正方形,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,∴
,∴![]() .
.
∴![]() ,∴
,∴![]() .
.
∵![]() ,∴当
,∴当![]() 时,
时,![]() 、
、![]() 、
、![]() 三点在一直线上时,
三点在一直线上时,
在![]() 中,∵
中,∵![]() ,∴
,∴![]() .
.
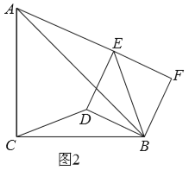
如图2,当点![]() 在线段
在线段![]() 上时,
上时,![]() ,∴
,∴![]() ;
;
如图3,当点![]() 在线段
在线段![]() 延长线上时,
延长线上时,![]() ,∴
,∴![]() .
.
综上所述,当![]() 时,线段
时,线段![]() 的长为
的长为![]() 或
或![]() ;
;

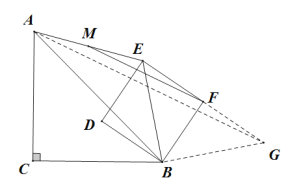
(3)延长EF到G使得FG=EF,连接AG,BG,
则△BFG为等腰直角三角形,
∴BG=![]() BF=
BF=![]() ,
,
∵M为AE中点,F为EG中点,
∴MF为△EAG中位线,
∴MF=![]() ,
,
在△ABG中,∵AB-BG≤AG≤AB+BG,
∴![]() ≤AG≤
≤AG≤![]() ,
,
∴![]() ≤MF≤
≤MF≤![]() .
.
本题为相似的综合题,考查了相似三角形的判定和性质,正方形,等腰直角三角形的性质,三角形中位线定理,三角形三边关系,解题关键是找到图形中的旋转相似,注意运用好分类讨论的数学思想,问题3中要善于构造中位线解决问题.


科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB∥DC,AB=AD,对角线AC.BD交于点O,AC平分∠BAD,过点C作CE⊥AB交AB的延长线于点E.连接OE.
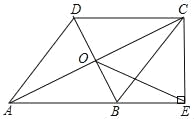
(1)求证:四边形ABCD是菱形;
(2)若AB=![]() .OE=2,求线段CE的长.
.OE=2,求线段CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为推广阳光体育“大课间”活动,我市某中学决定在学生中开设A:实心球.B:立定跳远,C:跳绳,D:跑步四种活动项目.为了了解学生对四种项目的喜欢情况,随机抽取了部分学生进行调查,并将调查结果绘制成如图①②的统计图.请结合图中的信息解答下列问题:
(1)在这项调查中,共调查了多少名学生?
(2)请计算本项调查中喜欢“立定跳远”的学生人数和所占百分比,并将两个统计图补充完整;
(3)若调查到喜欢“跳绳”的5名学生中有3名男生,2名女生.现从这5名学生中任意抽取2名学生.请用画树状图或列表的方法,求出刚好抽到同性别学生的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
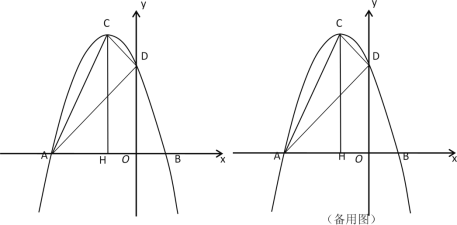
【题目】在平面直角坐标系中,抛物线![]() 与
与![]() 轴的两个交点分别为A(-3,0)、B(1,0),与y轴交于点D(0,3),过顶点C作CH⊥x轴于点H.
轴的两个交点分别为A(-3,0)、B(1,0),与y轴交于点D(0,3),过顶点C作CH⊥x轴于点H.
(1)求抛物线的解析式和顶点C的坐标;
(2)连结AD、CD,若点E为抛物线上一动点(点E与顶点C不重合),当△ADE与△ACD面积相等时,求点E的坐标;
(3)若点P为抛物线上一动点(点P与顶点C不重合),过点P向CD所在的直线作垂线,垂足为点Q,以P、C、Q为顶点的三角形与△ACH相似时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为进一步推动各级各类学校新型冠状病毒肺炎疫情防控工作,向广大教职工和学生普及新型冠状病毒肺炎疫情防控知识,做好师生返校前的卫生安全防护教育,上好开学第一课,省教育厅要求各级各类学校认真学习相关资料.某中学为了解学生的学习成果,对学生进行了新型冠状病毒肺炎防控知识测试,德育处随机从七、八两个年级各抽取20名学生的答卷成绩(单位:分)进行统计分析,过程如下:
收集数据
八年级:
85 | 80 | 95 | 100 | 90 | 95 | 85 | 65 | 75 | 85 |
90 | 90 | 70 | 90 | 100 | 80 | 80 | 90 | 95 | 75 |
七年级:
80 | 60 | 80 | 95 | 65 | 100 | 90 | 85 | 85 | 80 |
95 | 75 | 80 | 90 | 70 | 80 | 95 | 75 | 100 | 90 |
整理数据
成绩 |
|
|
|
|
八年级 | 2 | 5 |
|
|
七年级 | 3 | 7 | 5 | 5 |
分析数据
统计量 | 平均数 | 中位数 | 众数 |
八年级 | 85.75 | 87.5 |
|
七年级 | 83.5 |
| 80 |
应用数据
(1)填空:![]() __________,
__________,![]() __________,
__________,![]() __________,
__________,![]() __________;
__________;
(2)看完统计数据,你认为对新型冠状病毒肺炎防护知识掌握更好的年级是__________;
(3)若八年级共有500人参与答卷,请估计八年级成绩大于90分的人数;
(4)在这次测试中,八年级学生甲与七年级学生乙的成绩都是85分,请判断两人在各自年级的排名谁更靠前,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,∠EOF=60°,在射线OE上取一点A,使OA=10cm,在射线OF上取一点B,使OB=16cm.以OA、OB为邻边作平行四边形OACB.若点P在射线OF上,点Q在线段CA上,且CQ:OP=1:2.设CQ=a(a>0).

(1)连接PQ,当a=2时,求线段PQ的长度.
(2)若以点P、B、C、Q四点为顶点的四边形是平行四边形时,求a的值.
(3)连接PQ,以PQ所在的直线为对称轴,作点C关于直线PQ的对称点C',当点C′恰好落在平行四边形OACB的边上或者边所在的直线上时,直接写出a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有5张除正面数字外完全相同的卡片,正面数字分别为1,2,3,4,5,将卡片背面朝上洗匀,从中随机抽出一张记下数字后放回,洗匀后再次随机抽出一张,则抽出的两张卡片上所写数字相同的概率______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】位于湖北省荆州市滨江公园旁的万寿宝塔始建于明熹靖年间,周边风景秀丽.随着年代的增加,目前塔底低于地面约7米.某校学生先在地面![]() 处侧得塔顶的仰角为30°,再向古塔方向行进
处侧得塔顶的仰角为30°,再向古塔方向行进![]() 米后到达
米后到达![]() 处,在
处,在![]() 处侧得塔顶的仰角为45°(如图所示),已知古塔的整体高度约为40米,那么
处侧得塔顶的仰角为45°(如图所示),已知古塔的整体高度约为40米,那么![]() 的值为_________米.(结果保留根式)
的值为_________米.(结果保留根式)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】金松科技生态农业养殖有限公司种植和销售一种绿色羊肚菌,已知该羊肚菌的成本是12元/千克,规定销售价格不低于成本,又不高于成本的两倍.经过市场调查发现,某天该羊肚菌的销售量y(千克)与销售价格x(元/千克)的函数关系如下图所示:

(1)求y与x之间的函数解析式;
(2)求这一天销售羊肚菌获得的利润W的最大值;
(3)若该公司按每销售一千克提取1元用于捐资助学,且保证每天的销售利润不低于3600元,问该羊肚菌销售价格该如何确定.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com