
【题目】如图,矩形![]() 中,
中,![]() 为
为![]() 上一动点(
上一动点(![]() 与
与![]() 不重合),将
不重合),将![]() 沿
沿![]() 翻折至
翻折至![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,连接
,连接![]() 交
交![]() 于
于![]() ,若
,若![]() ,则
,则![]() 的长=______,折痕
的长=______,折痕![]() 的长_____.
的长_____.
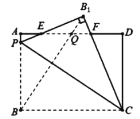
【答案】5 ![]()
【解析】
根据折叠及矩形的性质得到∠B1QF =∠CB1B,即可得到QF= B1F=5,如图,过点Q作QH⊥PB1于点H,得到△EHQ∽△EB1F,利用相似比得到EH,QH,从而得到B1H及B1Q,计算出cos∠HB1Q= ,根据等量代换得到∠PB1B=∠PBB1=∠PCB,利用cos∠PCB = cos∠HB1Q=
,根据等量代换得到∠PB1B=∠PBB1=∠PCB,利用cos∠PCB = cos∠HB1Q=![]() 即可计算得出PC的值.
即可计算得出PC的值.
解:由折叠可知,PC 垂直平分BB1,
∴BC=B1C,BP=B1P,
∴∠CBB1=∠CB1B,∠PBB1=∠PB1B
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠CBB1=∠B1QF,
∴∠B1QF =∠CB1B,
∴QF= B1F,
∵![]() ,
,
∴B1F=5,EF=13,
∴![]() ,
,
如图,过点Q作QH⊥PB1于点H,
∵∠PB1C=90°,
∴QH∥B1F,
∴△EHQ∽△EB1F,
∴![]() ,
,
即![]() ,
,
∴EH=![]() ,QH=
,QH=![]() ,
,
∴B1H=![]()
∴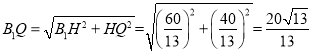 ,
,
∴cos∠HB1Q=
又∵∠PBB1+∠BPC=90°,∠BPC+∠PCB=90°,
∴∠PB1B=∠PBB1=∠PCB,
∴cos∠PCB = cos∠HB1Q=![]()
又∵![]() ,
,
∴cos∠PCB![]() ,即
,即![]() ,
,
∴PC=![]() ,
,
故答案为:5,![]()



 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】二次函数![]() 的图象与
的图象与![]() 轴交于
轴交于![]() 、
、![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),将二次函数
的左侧),将二次函数![]() 的图象绕点
的图象绕点![]() 旋转180度得到图象为
旋转180度得到图象为![]() ,当
,当![]() 时,图象
时,图象![]() 上点
上点![]() 纵坐标的最小值为
纵坐标的最小值为![]() ,则
,则![]() _________.
_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请分别在下列图中使用无刻度的直尺按要求画图.
(1)在图1中,点P是ABCD边AD上的中点,过点P画一条线段PM,使PM=![]() AB.
AB.
(2)在图2中,点A、D分别是BCEF边FB和EC上的中点,且点P是边EC上的动点,画出△PAB的一条中位线.
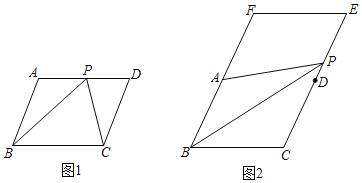
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明站在某广场一看台C处,从眼睛D处测得广场中心F的俯角为21°,若CD=1.6米,BC=1.5米,BC平行于地面FA,台阶AB的坡度为i=3:4,坡长AB=10米,则看台底端A点距离广场中心F点的距离约为(参考数据:sin21°≈0.36,cos21°≈0.93,tan21°≈0.38)( )
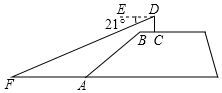
A.8.8米B.9.5米C.10.5米D.12米
查看答案和解析>>
科目:初中数学 来源: 题型:
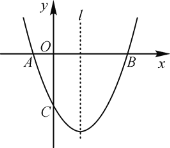
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)经过A(-1,0),B(3,0),C(0,-3)三点,直线l是抛物线的对称轴.
(1)求抛物线的函数解析式;
(2)设点M是直线l上的一个动点,当点M到点A,点C的距离之和最短时,求点M的坐标;
(3)在抛物线上是否存在点N,使S⊿ABN=![]() S⊿ABC,若存在,求出点N的坐标,若不存在,说明理由.
S⊿ABC,若存在,求出点N的坐标,若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋中装有![]() 个分别标有数
个分别标有数![]() 的小球,它们的形状、大小完全相同,小红先从口袋里随机摸出一个小球记下数为
的小球,它们的形状、大小完全相同,小红先从口袋里随机摸出一个小球记下数为![]() ,小颖在剩下的
,小颖在剩下的![]() 个球中随机摸出一个小球记下数为
个球中随机摸出一个小球记下数为![]() ,这样确定了点
,这样确定了点![]() 的坐标.
的坐标.![]()
(1)请你利用列表法或画树状图法求点![]() 的横、纵坐标均能被
的横、纵坐标均能被![]() 整除的概率.
整除的概率.
(2)记点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,求点
,求点![]() 位于反比例函数
位于反比例函数![]() 图象上的概率.
图象上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=x2+bx+c的对称轴为直线x=1,且经过点(﹣1,0).若关于x的一元二次方程x2+bx+c﹣t=0(t为实数)在﹣1<x<4的范围内有实数根,则t的取值范围是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
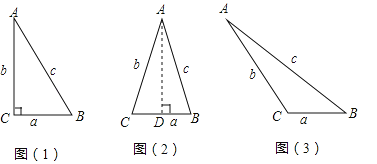
【题目】在△ABC中,BC=a,AC=b,AB=c,若∠C=90°,如图1,则有![]() ;若△ABC为锐角三角形时,小明猜想:
;若△ABC为锐角三角形时,小明猜想:![]() ,理由如下:如图2,过点A作AD⊥CB于点D,设CD=x.在Rt△ADC中,
,理由如下:如图2,过点A作AD⊥CB于点D,设CD=x.在Rt△ADC中,![]() ,在Rt△ADB中,
,在Rt△ADB中,![]() ,∴
,∴![]() .
.
∵a>0,x>0,∴2ax>0,∴![]() ,∴当△ABC为锐角三角形时
,∴当△ABC为锐角三角形时![]() .
.
所以小明的猜想是正确的.
(1)请你猜想,当△ABC为钝角三角形时, ![]() 与
与![]() 的大小关系.
的大小关系.
(2)温馨提示:在图3中,作BC边上的高.
(3)证明你猜想的结论是否正确.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com