
【题目】二次函数![]() 的图象与
的图象与![]() 轴交于
轴交于![]() 、
、![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),将二次函数
的左侧),将二次函数![]() 的图象绕点
的图象绕点![]() 旋转180度得到图象为
旋转180度得到图象为![]() ,当
,当![]() 时,图象
时,图象![]() 上点
上点![]() 纵坐标的最小值为
纵坐标的最小值为![]() ,则
,则![]() _________.
_________.
【答案】5
【解析】
根据二次函数解析式可求出A、B两点坐标,设图象G的解析式为y=-x2+bx+c,A点的对应点为A′,根据旋转的性质可求出点A′的坐标,把A′、B坐标代入可求出b、c的值,即可得图象G的解析式,可求出图象G的对称轴,根据二次函数的增减性即可得答案.
∵二次函数y=x2-4x-5的图象与x轴交于A、B两点(点A在点B的左侧),
∴y=0时,x2-4x-5=0,
解得x1=-1,x2=5,
∴A(-1,0),B(5,0),
∵将二次函数y=x2-4x-5的图象绕点B旋转180度得到图象为G,
∴设图象G的解析式为y=-x2+bx+c,A点的对应点为A′,
∴点A′坐标为(11,0),
把B、A′坐标代入y=-x2+bx+c得:![]() ,
,
解得:![]() ,
,
∴图象G点解析式为y=-x2+16x-55=-(x-8)2+9,
∴图象G的对称轴为直线x=8,
∵-1<0,
∴抛物线点开口向下,
∵9-8<8-6,
∴当![]() 时,x=6为函数最小值,
时,x=6为函数最小值,
∴点C纵坐标y=-36+96-55=5,
故答案为:5


科目:初中数学 来源: 题型:
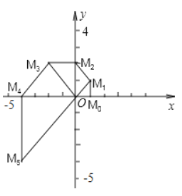
【题目】如图,在平面直角坐标系中,点![]() 的坐标为
的坐标为![]() ,将线段
,将线段![]() 绕原点
绕原点![]() 逆时针方向旋转
逆时针方向旋转![]() ,再将其延长至点
,再将其延长至点![]() ,使得
,使得![]() ,得到线段
,得到线段![]() ;又将线段
;又将线段![]() 绕原点
绕原点![]() 逆时针方向旋转
逆时针方向旋转![]() ,再将其延长至点
,再将其延长至点![]() ,使得
,使得![]() ,得到线段
,得到线段![]() ;如此下去,依次得到线段
;如此下去,依次得到线段![]() 、
、![]() 、
、![]() 、…根据以上规律,线段
、…根据以上规律,线段![]() 的长度为__
的长度为__
查看答案和解析>>
科目:初中数学 来源: 题型:
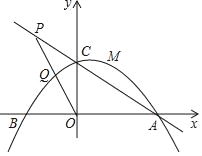
【题目】如图,抛物线y=﹣![]() (其中m>0)与x轴分别交于A,B两点(A在B的右侧),与y轴交于点c.
(其中m>0)与x轴分别交于A,B两点(A在B的右侧),与y轴交于点c.
(1)求△AOC的周长,(用含m的代数式表示)
(2)若点P为直线AC上的一点,且点P在第二象限,满足OP2=PCPA,求tan∠APO的值及用含m的代数式表示点P的坐标;
(3)在(2)的情况下,线段OP与抛物线相交于点Q,若点Q恰好为OP的中点,此时对于在抛物线上且介于点C与抛物线顶点之间(含点C与顶点)的任意一点M(x0,y0)总能使不等式n≤![]() 及不等式2n﹣
及不等式2n﹣![]() 恒成立,求n的取值范围.
恒成立,求n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某建筑物![]() 上挂着“巴山渝水,魅力重庆”的宣传条幅
上挂着“巴山渝水,魅力重庆”的宣传条幅![]() ,王同学利用测倾器在斜坡的底部
,王同学利用测倾器在斜坡的底部![]() 处测得条幅底部
处测得条幅底部![]() 的仰角为60°,沿斜坡AB走到B处测得条幅顶部C的仰角为50°.已知斜坡
的仰角为60°,沿斜坡AB走到B处测得条幅顶部C的仰角为50°.已知斜坡![]() 的坡度
的坡度![]() 米,
米,![]() 米(点
米(点![]() 在同平面内,
在同平面内,![]() ,测倾器的高度忽略不计),则条幅
,测倾器的高度忽略不计),则条幅![]() 的长度约为(参考数据:
的长度约为(参考数据:![]()
![]() )
)
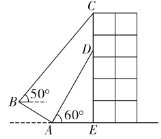
A.12.5米B.12.8米C.13.1米D.13.4米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在初中阶段的函数学习中,我们经历了“确定函数的表达式——利用函数图象研究其性质——应用函数解决问题”的学习过程.在画函数图象时,我们可以通过描点或平移的方法画出一个函数的大致图象,结合上面经历的学习过程,现在来解决下面问题:
在函数![]() 中,当
中,当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
(1)求这个函数的表达式;
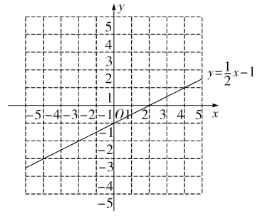
(2)在给出的平面直角坐标系中,请用你喜欢的方法画出这个函数的图象,并写出这个函数的一条性质;
(3)已知函数![]() 的图象如图所示,结合你所画的函数图象,直接写出不等式
的图象如图所示,结合你所画的函数图象,直接写出不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,二次函数![]() 的函数解析式为
的函数解析式为![]() ,点
,点![]() 是二次函数
是二次函数![]() 的图象上一点,过点
的图象上一点,过点![]() 作直线
作直线![]() 轴,且点
轴,且点![]() 的横坐标为
的横坐标为![]() ,二次函数
,二次函数![]() 的图象与二次函数
的图象与二次函数![]() 的图象关于直线
的图象关于直线![]() 成轴对称.
成轴对称.

(1)直接写出二次函数![]() 图象的对称轴(用含
图象的对称轴(用含![]() 的代数式表示)
的代数式表示)
(2)当点![]() 落在
落在![]() 轴上时,求二次函数
轴上时,求二次函数![]() 的解析式.
的解析式.
(3)当点![]() 在
在![]() 轴的右侧时,过点
轴的右侧时,过点![]() 作射线
作射线![]() 轴,设射线
轴,设射线![]() 与
与![]() 的图象交于点
的图象交于点![]() ,
,![]() 的图象在
的图象在![]() 上方的部分记为
上方的部分记为![]() ,
,![]() 的图象的剩余部分沿
的图象的剩余部分沿![]() 翻折得到
翻折得到![]() ,由
,由![]() 和
和![]() 所组成的图象记为
所组成的图象记为![]() .
.
①当点![]() 的纵坐标与横坐标之和为6时,求
的纵坐标与横坐标之和为6时,求![]() 的值
的值
②当![]() 时,随着
时,随着![]() 的增大,图象
的增大,图象![]() 所对应函数的函数值
所对应函数的函数值![]() 先减小后增大时,直接写出
先减小后增大时,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
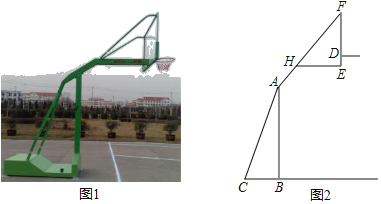
【题目】如图1,2分别是某款篮球架的实物图与示意图,AB⊥BC于点B,底座BC=1.3米,底座BC与支架AC所成的角∠ACB=60°,点H在支架AF上,篮板底部支架EH∥BC.EF⊥EH于点E,已知AH=![]() 米,HF=
米,HF=![]() 米,HE=1米.
米,HE=1米.
(1)求篮板底部支架HE与支架AF所成的∠FHE的度数.
(2)求篮板底部点E到地面的距离,(精确到0.01米)(参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】五一期间,甲、乙两人在附近的景点游玩,甲从![]() 、
、![]() 、
、![]() 三个景点中任意选择一个游玩,乙从
三个景点中任意选择一个游玩,乙从![]() 、
、![]() 两个景点中任意选择一个游玩.
两个景点中任意选择一个游玩.
(1)乙恰好游玩![]() 景点的概率为 ;
景点的概率为 ;
(2)用列表或画树状图的方法列出所有等可能的结果.并求甲、乙恰好游玩同一景点的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com