
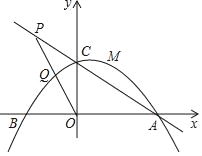
【题目】如图,抛物线y=﹣![]() (其中m>0)与x轴分别交于A,B两点(A在B的右侧),与y轴交于点c.
(其中m>0)与x轴分别交于A,B两点(A在B的右侧),与y轴交于点c.
(1)求△AOC的周长,(用含m的代数式表示)
(2)若点P为直线AC上的一点,且点P在第二象限,满足OP2=PCPA,求tan∠APO的值及用含m的代数式表示点P的坐标;
(3)在(2)的情况下,线段OP与抛物线相交于点Q,若点Q恰好为OP的中点,此时对于在抛物线上且介于点C与抛物线顶点之间(含点C与顶点)的任意一点M(x0,y0)总能使不等式n≤![]() 及不等式2n﹣
及不等式2n﹣![]() 恒成立,求n的取值范围.
恒成立,求n的取值范围.
【答案】(1) 3m+3![]() m;(2)tan∠APO=
m;(2)tan∠APO=![]() ,P(﹣
,P(﹣![]() );(3)
);(3) ![]() ≤n≤2.
≤n≤2.
【解析】
(1)分别令x=0和y=0,计算抛物线与两坐标轴的交点C和A的坐标,再根据勾股定理计算AC的长,根据三角形的周长可得结论;
(2)根据特殊三角函数值可得∠CAO=30°,证明△OPA∽△CPO,则∠POC=∠OAC=30°,可得tan∠APO=![]() ,过P作PE⊥x轴于E,表示OE和PE的长,根据点P在第二象限,可得P的坐标;
,过P作PE⊥x轴于E,表示OE和PE的长,根据点P在第二象限,可得P的坐标;
(3)根据中点坐标公式可得Q的坐标,代入抛物线的解析式可得m的值,计算对称轴,得x0的取值范围,根据两个不等式确定其解集即可.
(1)当x=0时,y=﹣![]() ×
×![]() ×(﹣3m)=
×(﹣3m)=![]() m,∴C(0,
m,∴C(0,![]() m),∴OC=
m),∴OC=![]() m,当y=0时,﹣
m,当y=0时,﹣![]() =0,解得:x1=﹣
=0,解得:x1=﹣![]() ,x2=3m.
,x2=3m.
∵A在B的右侧,其中m>0,∴A(3m,0),由勾股定理得:AC=![]() =
=![]() =2
=2![]() m,∴△AOC的周长=OA+OC+AC=3m+
m,∴△AOC的周长=OA+OC+AC=3m+![]() m+2
m+2![]() m=3m+3
m=3m+3![]() m;
m;
(2)Rt△AOC中,tan∠OAC=![]() =
=![]() =
=![]() ,∴∠CAO=30°.
,∴∠CAO=30°.
∵OP2=PCPA,∴![]() .
.
∵∠OPC=∠OPC,∴△OPA∽△CPO,∴∠POC=∠OAC=30°.
∵∠ACO=∠POC+∠APO,∴∠APO=60°﹣30°=30°,∴tan∠APO=![]() .
.
过P作PE⊥x轴于E.
∵∠APO=∠OAC=30°,∴PO=OA=3m,∠POE=60°,Rt△PEO中,∠EPO=30°,∴OE=![]() OP=
OP=![]() ,PE=
,PE=![]() .
.
∵点P在第二象限,∴P(﹣![]() );
);
(3)由(2)知:P(﹣![]() ).
).
∵点Q恰好为OP的中点,∴Q(﹣![]() ).
).
∵Q在抛物线上,则![]() =﹣
=﹣![]() ,解得:m=
,解得:m=![]() ,∴抛物线的解析式为:y=﹣
,∴抛物线的解析式为:y=﹣![]() (x+
(x+![]() )(x﹣3
)(x﹣3![]() )=﹣
)=﹣![]() ,对称轴是:x=﹣
,对称轴是:x=﹣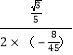 =
=![]() ,作抛物线的对称轴交抛物线于点F.
,作抛物线的对称轴交抛物线于点F.
∵M在点C与顶点F之间(含点C与顶点F),∴0≤x0≤![]() ,n≤
,n≤![]() ,设w1=
,设w1=![]() .
.
∵1>0,∴w1随x0的增大而增大,∴当x0=![]() 时,w1有最大值,即
时,w1有最大值,即![]() 有最小值为2,∴n≤2,对于不等式2n﹣
有最小值为2,∴n≤2,对于不等式2n﹣![]() ,n≥﹣2
,n≥﹣2![]() ,n≥﹣2(x0﹣
,n≥﹣2(x0﹣![]() )2+
)2+![]() ,设w2=﹣2(x0﹣
,设w2=﹣2(x0﹣![]() )2+
)2+![]() .
.
∵﹣2<0,∴w2有最大值.
∵0<![]() <
<![]() ,∴当x0=
,∴当x0=![]() 时,w2有最大值为
时,w2有最大值为![]() ,∴n≥
,∴n≥![]() .
.
综上所述:n的取值范围是![]() ≤n≤2.
≤n≤2.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
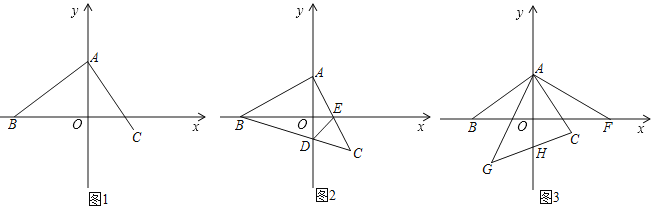
【题目】如图,点A(0,2)在y轴上,点B在x轴上,作∠BAC=90°,并使AB=AC.
(1)如图1,若点B的坐标为(﹣3,0),求点C的坐标.
(2)如图2,若点B的坐标为(﹣4,0),连接BC交y轴于点D,AC交x轴于点E,连接DE,求证:BE=AD+DE.
(3)在(1)的条件下,如图3,F为(4,0),作∠FAG=90°,并使AF=AG,连接GC交y轴于点H,求点H的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子里装有只有颜色不同的黑、白两种球共40个,小亮做摸球试验,他将盒子内的球搅匀后从中随机摸出一个球,记下颜色后放回,不断重复上述过程,对试验结果进行统计后,小玲得到下表中的数据:
摸球的次数n | 100 | 200 | 300 | 500 | 800 | 1000 | 1500 |
摸到白球的次数m | 70 | 128 | 171 | 302 | 481 | 599 | 903 |
摸到白球的频率 | 0.70 | 0.64 | 0.57 | 0.604 | 0.601 | 0.599 | 0.602 |
则下列结论中正确的是( )
A. n越大,摸到白球的概率越接近0.7
B. 当n=2000时,摸到白球的次数m=1200
C. 当n很大时,摸到白球的频率将会稳定在0.6附近
D. 这个盒子中约有28个白球
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】荣昌公司要将本公司100吨货物运往某地销售,经与春晨运输公司协商,计划租用甲,乙两种型号的汽车共6辆,用这6辆汽车一次将货物全部运走,其中每辆甲型汽车最多能装该种货物16吨,每辆乙型汽车最多能装该种货物18吨.已知租用1辆甲型汽车和2辆乙型汽车共需费用2500元;租用2辆甲型汽车和1辆乙型汽车共需费用2450元,且同一种型号汽车每辆租车费用相同.
(1)求租用一辆甲型汽车,一辆乙型汽车的费用分别是多少元?
(2)若荣昌公司计划此次租车费用不超过5000元.通过计算求出该公司有几种租车方案?请你设计出来,并求出最低的租车费用.
(3)该商业公司生产的此时令商品每件成本为15元,经过市场调研发现,这种商品在未来20天内的日销量m(件)与时间t(天)的函数关系:m=﹣2t+100;该商品每天的价格y(元/件)与时间t(天)的函数关系为:y=![]() t+20(1≤t≤20),其中t取整数;在实际销售的前20天中,该公司决定每销售一件商品就捐赠a元利润(a<4)给希望工程.公司通过销售记录发现,前20天中,每天扣除捐赠后的日销售利润时间t(天)的增大而增大(含20天的日销售利润和第19天的日销售利润相等的情况),求a的最小值.
t+20(1≤t≤20),其中t取整数;在实际销售的前20天中,该公司决定每销售一件商品就捐赠a元利润(a<4)给希望工程.公司通过销售记录发现,前20天中,每天扣除捐赠后的日销售利润时间t(天)的增大而增大(含20天的日销售利润和第19天的日销售利润相等的情况),求a的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把长方形纸片ABCD沿对角线折叠,设重叠部分为△EBD,那么,有下列说法:①△EBA和△EDC一定是全等三角形;②△EBD是等腰三角形,EB=ED;③折叠后得到的图形是轴对称图形;④折叠后∠ABE和∠CBD一定相等;其中正确的有( )

A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两个连接在一起的菱形的边长都是1cm,一只电子甲虫从点A开始按ABCDAEFGAB…的顺序沿菱形的边循环爬行,当电子甲虫爬行2014cm时停下,则它停的位置是( )

A. 点F B. 点E C. 点A D. 点C
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学课上,老师提出如下问题:
尺规作图:作一个角等于已知角
已知:∠AOB,
求作:∠A′OB′,使:∠A′OB′=∠AOB

小易同学作法如下:
①作射线O′A′;
②以点O为圆心,以任意长为半径作弧,交OA于C,交OB于D;
③以点O′为圆心,以OC长为半径作弧,交O′A于C
④以点C′圆心,以CD为半径作弧,交③中所画弧于D′;
⑤经过点D′作射线O′B′,∠A′O′B′就是所求的角.

老师说:“小易的作法正确”
请回答:小易的作图依据是______________________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
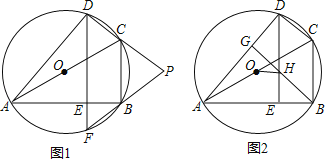
【题目】已知四边形ABCD是⊙O的内接四边形,AC是⊙O的直径,DE⊥AB,垂足为E.
(1)延长DE交⊙O于点F,延长DC,FB交于点P,如图1.求证:PC=PB;
(2)过点B作BG⊥AD,垂足为G,BG交DE于点H,且点O和点A都在DE的左侧,如图2.若AB=![]() ,DH=1,∠OHD=80°,求∠BDE的大小.
,DH=1,∠OHD=80°,求∠BDE的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com