
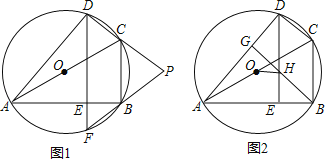
【题目】已知四边形ABCD是⊙O的内接四边形,AC是⊙O的直径,DE⊥AB,垂足为E.
(1)延长DE交⊙O于点F,延长DC,FB交于点P,如图1.求证:PC=PB;
(2)过点B作BG⊥AD,垂足为G,BG交DE于点H,且点O和点A都在DE的左侧,如图2.若AB=![]() ,DH=1,∠OHD=80°,求∠BDE的大小.
,DH=1,∠OHD=80°,求∠BDE的大小.
【答案】(1)详见解析;(2)∠BDE=20°.
【解析】
(1)根据已知条件易证BC∥DF,根据平行线的性质可得∠F=∠PBC;再利用同角的补角相等证得∠F=∠PCB,所以∠PBC=∠PCB,由此即可得出结论;(2)连接OD,先证明四边形DHBC是平行四边形,根据平行四边形的性质可得BC=DH=1,在Rt△ABC中,用锐角三角函数求出∠ACB=60°,进而判断出DH=OD,求出∠ODH=20°,再求得∠NOH=∠DOC=40°,根据三角形外角的性质可得∠OAD=![]() ∠DOC=20°,最后根据圆周角定理及平行线的性质即可求解.
∠DOC=20°,最后根据圆周角定理及平行线的性质即可求解.
(1)如图1,∵AC是⊙O的直径,
∴∠ABC=90°,
∵DE⊥AB,
∴∠DEA=90°,
∴∠DEA=∠ABC,
∴BC∥DF,
∴∠F=∠PBC,
∵四边形BCDF是圆内接四边形,
∴∠F+∠DCB=180°,
∵∠PCB+∠DCB=180°,
∴∠F=∠PCB,
∴∠PBC=∠PCB,
∴PC=PB;
(2)如图2,连接OD,
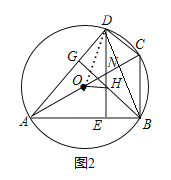
∵AC是⊙O的直径,
∴∠ADC=90°,
∵BG⊥AD,
∴∠AGB=90°,
∴∠ADC=∠AGB,
∴BG∥DC,
∵BC∥DE,
∴四边形DHBC是平行四边形,
∴BC=DH=1,
在Rt△ABC中,AB=![]() ,tan∠ACB=
,tan∠ACB=![]() ,
,
∴∠ACB=60°,
∴BC=![]() AC=OD,
AC=OD,
∴DH=OD,
在等腰△DOH中,∠DOH=∠OHD=80°,
∴∠ODH=20°,
设DE交AC于N,
∵BC∥DE,
∴∠ONH=∠ACB=60°,
∴∠NOH=180°﹣(∠ONH+∠OHD)=40°,
∴∠DOC=∠DOH﹣∠NOH=40°,
∵OA=OD,
∴∠OAD=![]() ∠DOC=20°,
∠DOC=20°,
∴∠CBD=∠OAD=20°,
∵BC∥DE,
∴∠BDE=∠CBD=20°.


科目:初中数学 来源: 题型:
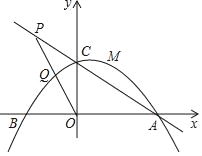
【题目】如图,抛物线y=﹣![]() (其中m>0)与x轴分别交于A,B两点(A在B的右侧),与y轴交于点c.
(其中m>0)与x轴分别交于A,B两点(A在B的右侧),与y轴交于点c.
(1)求△AOC的周长,(用含m的代数式表示)
(2)若点P为直线AC上的一点,且点P在第二象限,满足OP2=PCPA,求tan∠APO的值及用含m的代数式表示点P的坐标;
(3)在(2)的情况下,线段OP与抛物线相交于点Q,若点Q恰好为OP的中点,此时对于在抛物线上且介于点C与抛物线顶点之间(含点C与顶点)的任意一点M(x0,y0)总能使不等式n≤![]() 及不等式2n﹣
及不等式2n﹣![]() 恒成立,求n的取值范围.
恒成立,求n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
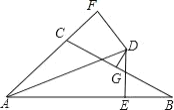
【题目】如图,△ABC 中, AB=11 , AC= 5 ,∠ BAC 的平分线 AD 与边 BC 的垂直平分线 CD 相 交于点 D ,过点 D 分别作 DE⊥AB ,DF⊥AC ,垂足分别为 E 、F ,则 BE 的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一儿童服装商店在销售中发现:某品牌童装平均每天可售出20件,每件盈利40元.为了迎接“六·一”儿童节,商店决定采取适当的降价措施,扩大销售量,增加盈利,尽快减少库存.经市场调查发现:如果每件童装降价1元,那么平均每天就可多售出2件.要想平均每天销售这种童装上盈利1200元,那么每件童装应降价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
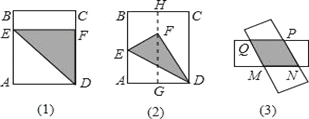
【题目】在一张长方形纸片ABCD中,AB=25cm,AD=20cm,现将这张纸片按下列图示方法折叠,请解决下列问题.
(1)如图(1),折痕为DE,点A的对应点F在CD上,求折痕DE的长;
(2)如图(2),H,G分别为BC,AD的中点,A的对应点F在HG上,折痕为DE,求重叠部分的面积;
(3)如图(3),在图(2)中,把长方形ABCD沿着HG对开,变成两张长方形纸片,按图示方式将两张纸片任意叠合后,判断重叠四边形的形状,并证明;
(4)在(3)中,重叠四边形的周长是否存在最大值或最小值?如果存在,试求出来;如果不存在,试简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在小明、小红两名同学中选拔一人参加2018年张家界市“经典诗词朗诵”大赛,在相同的测试条件下,两人5次测试成绩(单位:分)如下:
小明:80,85,82,85,83 小红:88,79,90,81,72.
回答下列问题:
(1)求小明和小红测试的平均成绩;
(2)求小明和小红五次测试成绩的方差.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将ABCD的AD边延长至点E,使DE=![]() AD,连接CE,F是BC边的中点,连接FD.
AD,连接CE,F是BC边的中点,连接FD.
(1)求证:四边形CEDF是平行四边形;
(2)若AB=3,AD=4,∠A=60°,求CE的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com