
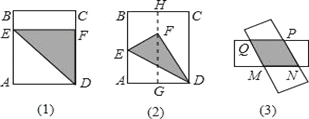
،¾جâؤ؟،؟شعز»صإ³¤·½ذخض½ئ¬ABCDضذ£¬AB=25cm£¬AD=20cm£¬دض½«صâصإض½ئ¬°´دآءذح¼ت¾·½·¨صغµ£¬اë½â¾ِدآءذختج⣮
£¨1£©بçح¼£¨1£©£¬صغ؛غخھDE£¬µمAµؤ¶شس¦µمFشعCDةد£¬اَصغ؛غDEµؤ³¤£»
£¨2£©بçح¼£¨2£©£¬H£¬G·ض±ًخھBC£¬ADµؤضذµم£¬Aµؤ¶شس¦µمFشعHGةد£¬صغ؛غخھDE£¬اَضطµ²؟·ضµؤأو»£»
£¨3£©بçح¼£¨3£©£¬شعح¼£¨2£©ضذ£¬°ر³¤·½ذخABCDرط×إHG¶ش؟ھ£¬±ن³ةء½صإ³¤·½ذخض½ئ¬£¬°´ح¼ت¾·½ت½½«ء½صإض½ئ¬بخزâµ؛د؛َ£¬إذ¶دضطµثؤ±كذخµؤذخ×´£¬²¢ض¤أ÷£»
£¨4£©شع£¨3£©ضذ£¬ضطµثؤ±كذخµؤضـ³¤تا·ٌ´وشع×î´َضµ»ٍ×îذ،ضµ£؟بç¹û´وشع£¬تشاَ³ِہ´£»بç¹û²»´وشع£¬تش¼ٍزھثµأ÷ہيسة.
،¾´ً°¸،؟£¨1£©20![]() cm£»£¨2£©
cm£»£¨2£©![]() £»£¨3£©ضطµثؤ±كذخMNPQµؤذخ×´تاءâذخ£¬ض¤أ÷¼û½âخِ£»£¨4£©ءâذخµؤ×î´َضـ³¤خھ58cm£®
£»£¨3£©ضطµثؤ±كذخMNPQµؤذخ×´تاءâذخ£¬ض¤أ÷¼û½âخِ£»£¨4£©ءâذخµؤ×î´َضـ³¤خھ58cm£®
،¾½âخِ،؟
£¨1£©¸ù¾فح¼ذخصغµµؤذشضت؟ةضھAD=AE=20cm£¬شظ¸ù¾ف¹´¹ة¶¨ہي¼´؟ةµأ³ِ½لآغ£»
£¨2£©سةصغµµؤذشضت؟ةµأµ½DG=![]() AD=
AD=![]() DE£¬شظ¸ù¾فض±½اب½اذخµؤذشضتµأ³ِ،دEDA=30،م£¬سةبٌ½اب½ا؛¯تµؤ¶¨زهµأµ½AEµؤ³¤£¬ہûسأب½اذخµؤأو»¹«ت½¼´؟ةµأ³ِ½لآغ£»
DE£¬شظ¸ù¾فض±½اب½اذخµؤذشضتµأ³ِ،دEDA=30،م£¬سةبٌ½اب½ا؛¯تµؤ¶¨زهµأµ½AEµؤ³¤£¬ہûسأب½اذخµؤأو»¹«ت½¼´؟ةµأ³ِ½لآغ£»
£¨3£©¸ù¾فئ½ذذثؤ±كذخµؤإذ¶¨ت×دبض¤µأثؤ±كذخMNPQتائ½ذذثؤ±كذخ£¬زٍخھء½جُ¾طذخµؤ؟ي¶بدàµب£¬ب»؛َ¸ù¾فئ½ذذثؤ±كذخMNPQµؤأو»¹«ت½¼´؟ةض¤µأثؤ±كذخµؤءع±كدàµب£¬½ّ¶ّض¤µأثؤ±كذختاءâذخ£»
£¨4£©µ±¾طذخض½ئ¬»¥دà´¹ض±ت±£¬صâ¸ِءâذخµؤضـ³¤×î¶ج£¬×îذ،ضµتا40cm£¬بçح¼2ثùت¾·إضأت±£¬ضطµ²؟·ضµؤءâذخأو»×î´َ£¬ةèGK=x£¬شٍHK=25-x£¬ہûسأ¹´¹ة¶¨ہي¼´؟ةاَ³ِxµؤضµ£¬½ّ¶ّ؟ةµأ³ِءâذخµؤضـ³¤£®
£¨1£©،كثؤ±كذخADFEتاص·½ذخ£¬
،àDE=![]() =
=![]() =20
=20![]() £¨cm£©
£¨cm£©
£¨2£©،كسةصغµ؟ةضھDG=![]() AD=
AD=![]() DF£¬
DF£¬
،àشعRt،÷DGFضذ£¬،دGFD=30،م£¬،دGDF=60،م£¬
،ك،دGDE=،دEDF£¬
،à،دEDA=30،م£®
،àشعRt،÷ADEضذ£¬AE=![]() AD
AD
،àسة¹´¹ة¶¨ہيµأAE==![]() £®
£®
،àS،÷DEF=![]() AEAD=
AEAD=![]() ،ء20،ء
،ء20،ء![]() =
=![]() £®
£®
£¨3£©ضطµثؤ±كذخMNPQµؤذخ×´تاءâذخ£»بçح¼1£¬
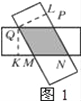
ض¤أ÷£؛زٍض½ئ¬¶¼تا¾طذخ£¬شٍضطµثؤ±كذخµؤ¶ش±ك»¥دàئ½ذذ£¬شٍثؤ±كذخMNPQتائ½ذذثؤ±كذخ£®
بçح¼1£¬¹Q×÷QL،حNPسعµمL£¬QK،حNMسعµمK£¬
سض،كQL=QK£¬
،àSMNPQ=PNQL=MNQK£®
،àMN=NP£¬
،àثؤ±كذخMNPQµؤذخ×´تاءâذخ£®
£¨4£©µ±¾طذخض½ئ¬»¥دà´¹ض±ت±£¬صâ¸ِءâذخµؤضـ³¤×î¶جتا40cm£®×î´َµؤءâذخبçح¼2ثùت¾·إضأت±£¬ضطµ²؟·ضµؤءâذخأو»×î´َ£®
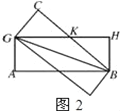
ةèGK=x£¬شٍHK=25©پx£®
شعRt،÷KHBضذ£¬x2=£¨25©پx£©2+102£¬
½âµأx=14.5£®
شٍءâذخµؤ×î´َضـ³¤خھ58 cm£®


 ؟خجأب«½â×ض´ت¾ن¶خئھصآدµءذ´ً°¸
؟خجأب«½â×ض´ت¾ن¶خئھصآدµءذ´ً°¸ ²½²½¸ك؟عثمجâ؟¨دµءذ´ً°¸
²½²½¸ك؟عثمجâ؟¨دµءذ´ً°¸
| ؤ꼶 | ¸كضذ؟خ³ج | ؤ꼶 | ³ُضذ؟خ³ج |
| ¸كز» | ¸كز»أâ·ر؟خ³جحئ¼ِ£، | ³ُز» | ³ُز»أâ·ر؟خ³جحئ¼ِ£، |
| ¸ك¶ | ¸ك¶أâ·ر؟خ³جحئ¼ِ£، | ³ُ¶ | ³ُ¶أâ·ر؟خ³جحئ¼ِ£، |
| ¸كب | ¸كبأâ·ر؟خ³جحئ¼ِ£، | ³ُب | ³ُبأâ·ر؟خ³جحئ¼ِ£، |
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟بçح¼£¬°ر³¤·½ذخض½ئ¬ABCDرط¶ش½ادكصغµ£¬ةèضطµ²؟·ضخھ،÷EBD£¬ؤاأ´£¬سذدآءذثµ·¨£؛¢ظ،÷EBA؛ح،÷EDCز»¶¨تاب«µبب½اذخ£»¢ع،÷EBDتاµبرüب½اذخ£¬EB£½ED£»¢غصغµ؛َµأµ½µؤح¼ذختاضل¶ش³ئح¼ذخ£»¢ـصغµ؛َ،دABE؛ح،دCBDز»¶¨دàµب£»ئنضذصب·µؤسذ( )

A. 1¸ِB. 2¸ِC. 3¸ِD. 4¸ِ
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟بçح¼£¬AB،خCD£¬EF½»ABسعE£¬½»CDسعF£¬EPئ½·ض،دAEF£¬FPئ½·ض،دCFE£¬ض±دكMN¾¹µمP²¢سëAB£¬CD·ض±ً½»سعµمM£¬N.
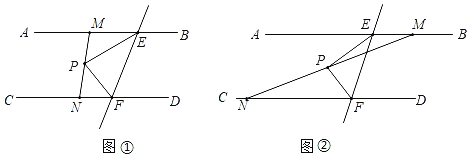
(1)بçح¼¢ظ£¬اَض¤£؛EM+FN£½EF£»
(2)بçح¼¢ع£¬(1)µؤ½لآغتا·ٌ³ةء¢£؟بô³ةء¢£¬اëض¤أ÷£»بô²»³ةء¢£¬ض±½سذ´³ِEM£¬FN£¬EFبجُدك¶خµؤتء؟¹طدµ.
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟دآءذ¹طسع¸إآتµؤثµ·¨£¬´يخَµؤتا£¨ £©
A. أ÷جىدآسêµؤ¸إآتتا80%£¬¼´أ÷جى80%µؤت±¼ن¶¼دآسꣻ
B. ×ِح¶ضہس²±زتشرéت±£¬ح¶ضہµؤ´خت×م¹»¶àت±£¬صأو³¯ةدµؤئµآت¾حش½½س½üسع![]() £»
£»
C. ،°13بثضذضءةظسذ2بثةْذ¤دàح¬،±£¬صâتاز»¸ِ±طب»تآ¼،£
D. ء¬ضہء½أ¶÷»×س£¬ثüأاµؤµمتدàح¬µؤ¸إآتتا![]() £»
£»
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟E،¢F·ض±ًتا±ك³¤خھ4µؤءâذخABCDضذ±كBC،¢CDةدµؤµم£¬،دB=،دEAF=60،م£¬،÷AEFµؤضـ³¤خھ![]() £¬شٍ
£¬شٍ![]() µؤ×îذ،ضµتا_______.
µؤ×îذ،ضµتا_______.
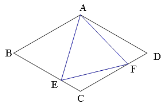
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟زرضھثؤ±كذخABCDتا،رOµؤؤع½سثؤ±كذخ£¬ACتا،رOµؤض±¾¶£¬DE،حAB£¬´¹×مخھE£®
£¨1£©رس³¤DE½»،رOسعµمF£¬رس³¤DC£¬FB½»سعµمP£¬بçح¼1£®اَض¤£؛PC=PB£»
£¨2£©¹µمB×÷BG،حAD£¬´¹×مخھG£¬BG½»DEسعµمH£¬ازµمO؛حµمA¶¼شعDEµؤ×َ²à£¬بçح¼2£®بôAB=![]() £¬DH=1£¬،دOHD=80،م£¬اَ،دBDEµؤ´َذ،£®
£¬DH=1£¬،دOHD=80،م£¬اَ،دBDEµؤ´َذ،£®
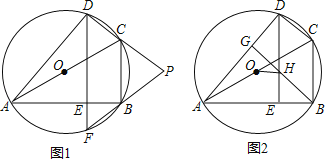
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟بçح¼£¬شع¾طذخABCDضذ£¬EتاABµؤضذµم£¬ء¬½سDE،¢CE£®
£¨1£©اَض¤£؛،÷ADE،ص،÷BCE£»
£¨2£©بôAB=6£¬AD=4£¬اَ،÷CDEµؤضـ³¤£®

²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟بçح¼£¬تاسة27¸ِدàح¬µؤذ،ء¢·½؟é´î³ةµؤ¼¸؛خجه£¬ثüµؤب¸ِتسح¼تا3،ء3µؤص·½ذخ£¬بôؤأµôبô¸ة¸ِذ،ء¢·½؟飨¼¸؛خجه²»µ¹µô£©£¬ئنب¸ِتسح¼بش¶¼خھ3،ء3µؤص·½ذخ£¬شٍ×î¶àؤـؤأµôذ،ء¢·½؟éµؤ¸ِتخھ£¨،،،،£©

A. 10 B. 12 C. 15 D. 18
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟2018ؤêؤ³تذ¸كضذصذةْجهس؟¼تش¹و¶¨£؛¾إؤ꼶ؤذةْ؟¼تشدîؤ؟سذA،¢B،¢C،¢D،¢Eخهہà£؛ئنضذA£؛1000أ×إـ![]() ±ط؟¼دîؤ؟
±ط؟¼دîؤ؟![]() £»B£؛جّة£»C£؛زجهدٍةد£»D£؛ء¢¶¨جّش¶£»E£؛50أ×إـ£¬شظ´سB،¢C،¢D،¢Eضذ¸÷ر،ء½دî½ّذذ؟¼تش£®
£»B£؛جّة£»C£؛زجهدٍةد£»D£؛ء¢¶¨جّش¶£»E£؛50أ×إـ£¬شظ´سB،¢C،¢D،¢Eضذ¸÷ر،ء½دî½ّذذ؟¼تش£®
![]() بôؤذةْ¼×µعز»´خر،ز»دض±½سذ´³ِؤذةْ¼×ر،ضذدîؤ؟Eµؤ¸إآت£®
بôؤذةْ¼×µعز»´خر،ز»دض±½سذ´³ِؤذةْ¼×ر،ضذدîؤ؟Eµؤ¸إآت£®
![]() بô¼×،¢ززء½أû¾إؤ꼶ؤذةْشعر،دîµؤ¹³جضذ£¬µعز»´خ¶¼تار،ءثدîؤ؟E£¬ؤاأ´ثûء©µع¶´خح¬ت±ر،شٌجّة»ٍء¢¶¨جّش¶µؤ¸إآتتا¶àةظ£؟اëسأءذ±ي·¨»ٍ»ت÷×´ح¼µؤ·½·¨¼سزشثµأ÷²¢ءذ³ِثùسذµب؟ةؤـµؤ½ل¹û£®
بô¼×،¢ززء½أû¾إؤ꼶ؤذةْشعر،دîµؤ¹³جضذ£¬µعز»´خ¶¼تار،ءثدîؤ؟E£¬ؤاأ´ثûء©µع¶´خح¬ت±ر،شٌجّة»ٍء¢¶¨جّش¶µؤ¸إآتتا¶àةظ£؟اëسأءذ±ي·¨»ٍ»ت÷×´ح¼µؤ·½·¨¼سزشثµأ÷²¢ءذ³ِثùسذµب؟ةؤـµؤ½ل¹û£®
²é؟´´ً°¸؛ح½âخِ>>
¹ْ¼تر§ذ£سإر، - ء·د°²لءذ±ي - تشجâءذ±ي
؛±±ت،»¥ءھحّخ¥·¨؛ح²»ء¼ذإد¢¾ظ±¨ئ½ج¨ | حّةدسذ؛¦ذإد¢¾ظ±¨×¨اّ | µçذإص©ئ¾ظ±¨×¨اّ | ةوہْت·ذéخقض÷زهسذ؛¦ذإد¢¾ظ±¨×¨اّ | ةوئَاضب¨¾ظ±¨×¨اّ
خ¥·¨؛ح²»ء¼ذإد¢¾ظ±¨µç»°£؛027-86699610 ¾ظ±¨ستدن£؛58377363@163.com