练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】在矩形ABCD中，点E在BC上，AE=AD，DF⊥AE，垂足为F．

    （1）求证．DF=AB；

    （2）若∠FDC=30°，且AB=4，求AD．

    【答案】(1)详见解析;(2)8.

    【解析】

    （1）利用“AAS”证△ADF≌△EAB即可得；

    （2）由∠ADF+∠FDC=90°、∠DAF+∠ADF=90°得∠FDC=∠DAF=30°，据此知AD=2DF，根据DF=AB可得答案．

    （1）在矩形ABCD中，∵AD∥BC，

    ∴∠AEB=∠DAF，

    又∵DF⊥AE，

    ∴∠DFA=90°，

    ∴∠DFA=∠B，

    又∵AD=EA，

    ∴△ADF≌△EAB，

    ∴DF=AB；

    （2）∵∠ADF+∠FDC=90°，∠DAF+∠ADF=90°，

    ∴∠FDC=∠DAF=30°，

    ∴AD=2DF，

    ∵DF=AB，

    ∴AD=2AB=8．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，两个连接在一起的菱形的边长都是1cm，一只电子甲虫从点A开始按ABCDAEFGAB…的顺序沿菱形的边循环爬行，当电子甲虫爬行2014cm时停下，则它停的位置是(　 　)

    A. 点F B. 点E C. 点A D. 点C

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】设a，b，c是△ABC的三条边，关于x的方程x2+x+c-a=0有两个相等的实数根，方程3cx+2b=2a的根为x=0.

    （1）试判断△ABC的形状；

    （2）若a，b为方程x2+mx-3m=0的两个根，求m的值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读下面的例题，范例：解方程，

    解：（1）当≥0时，原方程化为，解得：，（不合题意，舍去）．

    （2）当＜0时，原方程化为，解得：，（不合题意，舍去）．

    ∴原方程的根是，

    请参照例题解方程．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

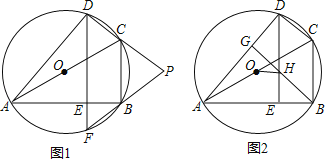
    【题目】已知四边形ABCD是⊙O的内接四边形，AC是⊙O的直径，DE⊥AB，垂足为E．

    （1）延长DE交⊙O于点F，延长DC，FB交于点P，如图1．求证：PC=PB；

    （2）过点B作BG⊥AD，垂足为G，BG交DE于点H，且点O和点A都在DE的左侧，如图2．若AB= ，DH=1，∠OHD=80°，求∠BDE的大小．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：如图，在中，，平分，，，那么的长是 ____________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图,在⊙O中,点C是优弧ACB的中点,D、E分别是OA、OB上的点,且AD=BE,弦CM、CN分别过点D、E.

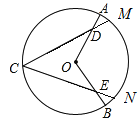
    (1)求证：CD=CE．

    (2)求证：=.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知： 平分， 垂直平分， ， ，垂足分别是点、．求证(1) ；(2) ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知函数是关于的二次函数，求：

    求满足条件的值；

    当抛物线开口向下时，请写出此时抛物线的顶点坐标；

    为何值时，抛物线有最小值？最小值是多少？当为何值时，随的增大而增大？

    查看答案和解析>>

    同步练习册答案