
【题目】如图,已知: ![]() 平分
平分![]() ,
, ![]() 垂直平分
垂直平分![]() ,
, ![]() ,
, ![]() ,垂足分别是点
,垂足分别是点![]() 、
、![]() .求证(1)
.求证(1) ![]() ;(2)
;(2) ![]() .
.

【答案】(1)证明见解析;(2)证明见解析.
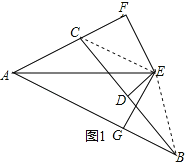
【解析】试题分析:(1)连接CE、BE,根据线段垂直平分线的性质得到EC=EB,根据角平分线的性质得到EF=EG,于是证得Rt△CFE≌Rt△BGE,即可得到结论;
(2)根据AE平分∠BAC,EF⊥AC,EG⊥AB,得到EF=EG,证得Rt△AGE≌Rt△AFE,得到AG=AF,于是得到结论.
试题解析:证明:(1)连接CE、BE,∵ED垂直平分BC,∴EC=EB,∵AE平分∠CAB,EF⊥AC,EG⊥AB,∴EF=EG,在Rt△CFE和Rt△BGE中,∵EC=EB,EF=EG,∴Rt△CFE≌Rt△BGE,∴BG=CF;
(2)∵AE平分∠BAC,EF⊥AC,EG⊥AB,∴EF=EG,在Rt△AGE和Rt△AFE中,∵AE=AE,EG=EF,∴Rt△AGE≌Rt△AFE,∴AG=AF,∵AB=AG+BG,∴AB=AF+CF.


科目:初中数学 来源: 题型:
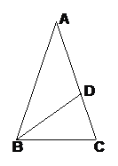
【题目】如图,已知△ABC中,D是AC边上一点,∠A=36,∠C=72,∠ADB=108。
求证:(1)AD=BD=BC;
(2)点D是线段AC的黄金分割点。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中, 边AB的垂直平分线交对角线AC于点F,垂足为点E,连结DF,若∠BAD=80°,则∠CDF的度数为( )
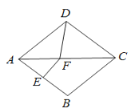
A.80°B.70°C.65°D.60°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了改善市民的生活环境,我是在某河滨空地处修建一个如图所示的休闲文化广场.在Rt△ABC内修建矩形水池DEFG,使顶点D、E在斜边AB上,F、G分别在直角边BC、AC上;又分别以AB、BC、AC为直径作半圆,它们交出两弯新月(图中阴影部分),两弯新月部分栽植花草;其余空地铺设地砖.其中![]() 米,∠BAC=600.设EF=x米,DE=y米.
米,∠BAC=600.设EF=x米,DE=y米.
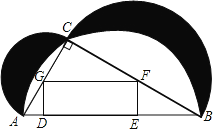
(1)求y与x之间的函数解析式;
(2)当x为何值时,矩形DEFG的面积最大?最大面积是多少?
(3)求两弯新月(图中阴影部分)的面积,并求当x为何值时,矩形DEFG的面积等于两弯新月面积的![]() ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】6月1日起,我国将全面试行居民阶梯式电价,某市出台了实施细则,具体规定如下:
设用电量为a度,当a≤150时,电价为现行电价,每度0.51元;当150<a≤240时,在现行电价基础上,每度提高0.05元;当a>240时,在现行电价基础上,每度提高0.30元.设某户的月用电量为x(度),电费为y(元).则y与x之间的函数关系的大致图像是( )
A. B.
B.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂家在甲、乙两家商场销售同一商品所获得的利润分别为![]() ,
,![]() (单位:元),
(单位:元),![]() ,
,![]() 与销售数量x(单位:件)的函数关系如图所示,试根据图象解决下列问题:
与销售数量x(单位:件)的函数关系如图所示,试根据图象解决下列问题:
(1)分别求出![]() ,
,![]() 关于x的函数关系式;
关于x的函数关系式;
(2)现厂家分配该商品800件给甲商场,400件给乙商场,当甲、乙商场售完这批商品后,厂家可获得的总利润是多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个转盘被分成![]() 等分,每一份上各写有一个数字,随机转动转盘
等分,每一份上各写有一个数字,随机转动转盘![]() 次,第一次转到的数字数字为十位数字,第二次转到的数字为个位数字,
次,第一次转到的数字数字为十位数字,第二次转到的数字为个位数字,![]() 次转动后组成一个两位数(若指针停在等分线上则重新转一次)
次转动后组成一个两位数(若指针停在等分线上则重新转一次)
![]() 用画树状图的方法求出转动后所有可能出现的两位数的个数.
用画树状图的方法求出转动后所有可能出现的两位数的个数.
![]() 甲、乙两人做游戏,约定得到的两位数是偶数时甲胜,否则乙胜,这个游戏公平吗?请说明理由.
甲、乙两人做游戏,约定得到的两位数是偶数时甲胜,否则乙胜,这个游戏公平吗?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两单位为爱心基金捐款,其中甲单位捐款4800元,乙单位捐款6000元,已知乙单位捐款人数比甲单位多30人,且两单位人均捐款数相等,问这两单位一共有多少人?人均捐款额是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com