
【题目】已知函数![]() 是关于
是关于![]() 的二次函数,求:
的二次函数,求:
![]() 求满足条件的
求满足条件的![]() 值;
值;
![]() 当抛物线开口向下时,请写出此时抛物线的顶点坐标;
当抛物线开口向下时,请写出此时抛物线的顶点坐标;
![]() 为何值时,抛物线有最小值?最小值是多少?当
为何值时,抛物线有最小值?最小值是多少?当![]() 为何值时,
为何值时,![]() 随
随![]() 的增大而增大?
的增大而增大?
科目:初中数学 来源: 题型:
【题目】我市某企业接到一批产品的生产任务,按要求必须在14天内完成.已知每件产品的出厂价为60元.工人甲第x天生产的产品数量为y件,y与x满足如下关系:
![]()
(1)工人甲第几天生产的产品数量为70件?
(2)设第x天生产的产品成本为P元/件,P与![]() 的函数图象如图.工人甲第x天创造的利润为W元,求W与x的函数关系式,并求出第几天时利润最大,最大利润是多少?
的函数图象如图.工人甲第x天创造的利润为W元,求W与x的函数关系式,并求出第几天时利润最大,最大利润是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着地铁和共享单车的发展,“地铁![]() 单车”已成为很多市民出行的选择
单车”已成为很多市民出行的选择![]() 张老师从学校站出发,先乘坐地铁到某一站出地铁,再骑共享单车回家,设他出地铁的站点与学校距离为
张老师从学校站出发,先乘坐地铁到某一站出地铁,再骑共享单车回家,设他出地铁的站点与学校距离为![]() 单位:千米
单位:千米![]() ,乘坐地铁的时间为
,乘坐地铁的时间为![]() 单位分钟
单位分钟![]() ,经测量,得到如下数据:
,经测量,得到如下数据:
地铁站 | A | B | C | D |
| E |
| 6 |
| 10 | |
| 15 |
| 9 | 12 | a | 20 |
| b |
![]() 根据表中数据的规律,直接写出表格中a、b的值和
根据表中数据的规律,直接写出表格中a、b的值和![]() 关于x的函数表达式;
关于x的函数表达式;
![]() 张老师骑单车的时间
张老师骑单车的时间![]() 单位:分钟
单位:分钟![]() 也受x的影响,其关系可以用
也受x的影响,其关系可以用![]() 米描述,
米描述,
![]() 若张老师出地铁的站点与学校距离为14千米,请求出张老师从学校回到家所需的时间;
若张老师出地铁的站点与学校距离为14千米,请求出张老师从学校回到家所需的时间;
![]() 若张老师准备在离家较近的A,B,C,D,E中的某一站出地铁,请问:张老师应选择在哪一站出地铁,才能使他从学校回到家所需的时间最短?并求出最短时间.
若张老师准备在离家较近的A,B,C,D,E中的某一站出地铁,请问:张老师应选择在哪一站出地铁,才能使他从学校回到家所需的时间最短?并求出最短时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将ABCD的AD边延长至点E,使DE=![]() AD,连接CE,F是BC边的中点,连接FD.
AD,连接CE,F是BC边的中点,连接FD.
(1)求证:四边形CEDF是平行四边形;
(2)若AB=3,AD=4,∠A=60°,求CE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:直线y=![]() x+3与x轴、y轴分别相于点A和点B,点C在线段AO上.
x+3与x轴、y轴分别相于点A和点B,点C在线段AO上.
将△CBO沿BC折叠后,点O恰好落在AB边上点D处
(1)求直线BC的解析式;
(2)求点D的坐标;
(3)P为平面内一动点,且以A、B、C、P为顶点的四边形为平行四边形,直接写出点P坐标 .
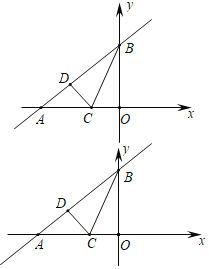
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解题
(1)阅读理解:如图①,等边![]() 内有一点
内有一点![]() ,若点
,若点![]() 到顶点
到顶点![]() ,
,![]() ,
,![]() 的距离分别为3,4,5,求
的距离分别为3,4,5,求![]() 的大小.
的大小.
思路点拨:考虑到![]() ,
,![]() ,
,![]() 不在一个三角形中,采用转化与化归的数学思想,可以将
不在一个三角形中,采用转化与化归的数学思想,可以将![]() 绕顶点
绕顶点![]() 逆时针旋转
逆时针旋转![]() 到
到![]() 处,此时
处,此时![]() ,这样,就可以利用全等三角形知识,结合已知条件,将三条线段的长度转化到一个三角形中,从而求出
,这样,就可以利用全等三角形知识,结合已知条件,将三条线段的长度转化到一个三角形中,从而求出![]() 的度数.请你写出完整的解题过程.
的度数.请你写出完整的解题过程.
(2)变式拓展:请你利用第(1)题的解答思想方法,解答下面问题:
已知如图②,![]() 中,
中,![]() ,
,![]() ,
,![]() 、
、![]() 为
为![]() 上的点且
上的点且![]() ,
,![]() ,
,![]() ,求
,求![]() 的大小.
的大小.
(3)能力提升:如图③,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 为
为![]() 内一点,连接
内一点,连接![]() ,
,![]() ,
,![]() ,且
,且![]() ,请直接写出
,请直接写出![]() 的值,即
的值,即![]() ______.
______.
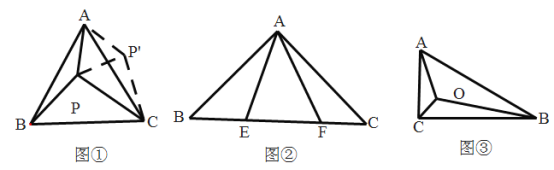
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC内接于⊙O,过点A作直线EF.
(1)如图①,AB是直径,要使EF是⊙O的切线,还须添加一个条件是(只需写出三种情况).
(ī) (īī) (īīī)
(2)如图(2),若AB为非直径的弦,∠CAE=∠B,则EF是⊙O的切线吗?为什么?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com