
【题目】已知△ABC内接于⊙O,过点A作直线EF.
(1)如图①,AB是直径,要使EF是⊙O的切线,还须添加一个条件是(只需写出三种情况).
(ī) (īī) (īīī)
(2)如图(2),若AB为非直径的弦,∠CAE=∠B,则EF是⊙O的切线吗?为什么?

【答案】(1)AB⊥EF ∠BAE=90° ∠ABC=∠EAC(2)详见解析
【解析】
(1)根据切线的判断由![]() 或
或![]() 可判断
可判断![]() 为
为![]() 的切线;当
的切线;当![]() ,根据圆周角定理得
,根据圆周角定理得![]() ,所以
,所以![]() ,即
,即![]() ,于是也可判断
,于是也可判断![]() 为
为![]() 的切线;
的切线;
(2)作直径![]() ,连结
,连结![]() ,由
,由![]() 为直径得
为直径得![]() ,则
,则![]() ,根据圆周角定理得
,根据圆周角定理得![]() ,而
,而![]() ,所以
,所以![]() ,则
,则![]() ,根据切线的判定定理得到
,根据切线的判定定理得到![]() 为
为![]() 的切线.
的切线.
(1)当 AB⊥EF 或∠BAE=90°可判断 EF 为⊙O 的切线;
当∠ABC=∠EAC,∵AB 为直径,
∴∠ACB=90°,
∴∠ABC+∠CAB=90°,
∴∠EAC+∠CAB=90°,
∴AB⊥EF,
∴EF 为⊙O 的切线;
故答案为 AB⊥EF、∠BAE=90°、∠ABC=∠EAC;
(2)证明:作直径 AD,连结 CD,
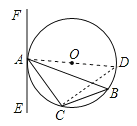
∵AD 为直径,
∴∠ACD=90°,
∴∠D+∠CAD=90°,
![]()
![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴EF 为⊙O 的切线.


 灵星计算小达人系列答案
灵星计算小达人系列答案科目:初中数学 来源: 题型:
【题目】已知函数![]() 是关于
是关于![]() 的二次函数,求:
的二次函数,求:
![]() 求满足条件的
求满足条件的![]() 值;
值;
![]() 当抛物线开口向下时,请写出此时抛物线的顶点坐标;
当抛物线开口向下时,请写出此时抛物线的顶点坐标;
![]() 为何值时,抛物线有最小值?最小值是多少?当
为何值时,抛物线有最小值?最小值是多少?当![]() 为何值时,
为何值时,![]() 随
随![]() 的增大而增大?
的增大而增大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BA=BC,D在边CB上,且DB=DA=AC
(1)填空:如图1,∠B= °,∠C= °;
(2)如图2,若M为线段BC上的点,过M作MH⊥AD,交AD的延长线于点H,分别交直线AB、AC与点N、E.
①求证:△ANE是等腰三角形;
②线段BN、CE、CD之间的数量关系是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,∠ABC=30°,AC=1,△ABC绕点C顺时针旋转一定角度得到△DEC,点D恰好落在AB边上,连接AE. 求:
(1)旋转角的度数;
(2)AE的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,C,D,E在Rt△MON的边上,∠MON=90°,AE⊥AB且AE=AB,BC⊥CD,BH⊥ON于点H,DF⊥ON于点F,OM=12,OE=6,BH=3,DF=4,FN=8,图中阴影部分的面积为( )

A. 30 B. 50 C. 66 D. 80
查看答案和解析>>
科目:初中数学 来源: 题型:
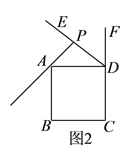
【题目】在正方形![]() 中,
中,![]() 为正方形的外角
为正方形的外角![]() 的角平分线,点
的角平分线,点![]() 在线段
在线段![]() 上,过点
上,过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,交射线
,交射线![]() 于点
于点![]() .
.
(![]() )如图1,若点
)如图1,若点![]() 与点
与点![]() 重合.
重合.
①依题意补全图1.
②判断![]() 与
与![]() 的数量关系并加以证明.
的数量关系并加以证明.
(![]() )如图2,若点
)如图2,若点![]() 恰好在线段
恰好在线段![]() 上,正方形
上,正方形![]() 的边长为
的边长为![]() ,请写出求
,请写出求![]() 长的思路(可以不写出计算结果).
长的思路(可以不写出计算结果).

查看答案和解析>>
科目:初中数学 来源: 题型:
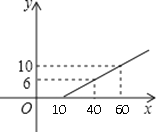
【题目】某长途汽车客运公司规定旅客可以免费携带一定质量的行李,当行李的质量超过规定时,需付的行李费y(元)与行李质量x(kg)之间的函数表达式为![]() ,这个函数的图像如图所示,求:
,这个函数的图像如图所示,求:
(1)k和b的值;
(2)旅客最多可免费携带行李的质量;
(3)行李费为4~15元时,旅客携带行李的质量为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
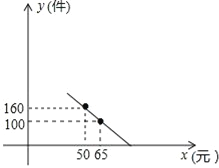
【题目】某商场老板对一种新上市商品的销售情况进行记录,已知这种商品进价为每件40元,经过记录分析发现,当销售单价在40元至90元之间(含40元和90元)时,每月的销售量y(件)与销售单价x(元)之间的关系可近似地看作一次函数,其图象如图所示.
(1)求y与x的函数关系式.
(2)设商场老板每月获得的利润为P(元),求P与x之间的函数关系式;
(3)如果想要每月获得2400元的利润,那么销售单价应定为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com