
【题目】某长途汽车客运公司规定旅客可以免费携带一定质量的行李,当行李的质量超过规定时,需付的行李费y(元)与行李质量x(kg)之间的函数表达式为![]() ,这个函数的图像如图所示,求:
,这个函数的图像如图所示,求:
(1)k和b的值;
(2)旅客最多可免费携带行李的质量;
(3)行李费为4~15元时,旅客携带行李的质量为多少?
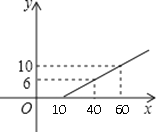
【答案】(1)k=0.02;b=-2;(2)旅客最多可免费携带行李的10千克;(3)行李费为4~15元时,旅客携带行李的质量为30~85千克
【解析】试题(1)利用待定系数法求一次函数解析式解答;
(2)令y=0时求出x的值即可;
(3)分别求出x=4、15时的x的取值范围,然后根据一次函数的增减性解答即可.
试题解析:(1)由图可知,函数图象经过点(40,6),(60,10),
所以![]() ,
,
解得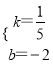 ;
;
(2)令y=0,则![]() ,
,
解得x=10,
所以,旅客最多可免费携带行李的质量为10kg;
(3)令y=4,则![]() ,解得x=30,
,解得x=30,
令y=15,则![]() ,解得x=85,
,解得x=85,
所以行李费为4~15元时,旅客携带行李的质量为30~85.


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:初中数学 来源: 题型:
【题目】已知△ABC内接于⊙O,过点A作直线EF.
(1)如图①,AB是直径,要使EF是⊙O的切线,还须添加一个条件是(只需写出三种情况).
(ī) (īī) (īīī)
(2)如图(2),若AB为非直径的弦,∠CAE=∠B,则EF是⊙O的切线吗?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:三角形ABC中,∠A=90,AB=AC,D为BC的中点,如图,E,F分别是AB,AC上的点,且BE=AF,求证:△DEF为等腰直角三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,△ACB与△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,点D为AB边上的一点.
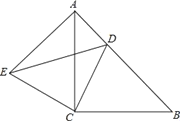
(1)求证:△BCD≌△ACE;
(2)若AD=3,BD=4,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面的图象反映的过程是:张强从家跑步去体育场,在那里锻炼了一阵后又原路返回,顺路到文具店去买笔,然后散步回家.其中x表示时间,y表示张强离家的距离.根据图象回答:
(1)体育场离张强家的多远?张强从家到体育场用了多长时间?
(2)体育场离文具店多远?
(3)张强在文具店逗留了多久?
(4)计算张强从文具店回家的平均速度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,假命题的是( )
A.在△ABC中,若∠B+∠C=∠A,则△ABC是直角三角形
B.在△ABC中,若a2=(b+c)(b﹣c),则△ABC是直角三角形
C.在△ABC中,若∠A:∠B:∠C=1:2:3,则△ABC是直角三角形
D.在△ABC中,若a=32,b=42,c=52,则△ABC是直角三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC=12厘米,BC=9厘米,点D为AB的中点,如果点P在线段BC上以v厘米/秒的速度由B点向C点运动,同时点Q在线段CA上由C点向A点运动。若点Q的运动速度为3厘米/秒,则当△BPD与△CQP全等时,v的值为_____________
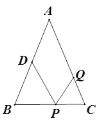
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解题
在平面直角坐标系xOy中,点P(x0,y0)到直线Ax+By+C=0(A2+B2≠0)的距离公式为:d=![]() ,
,
例如,求点P(1,3)到直线4x+3y﹣3=0的距离.
解:由直线4x+3y﹣3=0知:A=4,B=3,C=﹣3
所以P(1,3)到直线4x+3y﹣3=0的距离为:d=![]() =2
=2
根据以上材料,解决下列问题:
(1)求点P1(0,0)到直线3x﹣4y﹣5=0的距离.
(2)若点P2(1,0)到直线x+y+C=0的距离为![]() ,求实数C的值.
,求实数C的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com