
【题目】如图所示,△ACB与△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,点D为AB边上的一点.
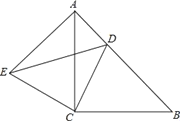
(1)求证:△BCD≌△ACE;
(2)若AD=3,BD=4,求DE的长.
【答案】(1)见解析;(2)5
【解析】
(1)根据同角的余角相等得到∠ACE=∠BCD,又夹这个角的两边分别是两等腰直角三角形的腰,利用SAS即可证明;
(2)根据全等三角形的对应边相等、对应角相等可以得到AE=BD,∠EAC=∠B=45°,所以△AED是直角三角形,利用勾股定理即可求出DE长度.
(1)证明:∵△ACB和△ECD都是等腰直角三角形,
∴AC=BC,EC=DC.
∵∠ACE=∠DCE-∠DCA,∠BCD=∠ACB-∠DCA,
∠ACB=∠ECD=90°,
∴∠ACE=∠BCD.
在△ACE和△BCD中
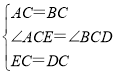 ,
,
∴△ACE≌△BCD(SAS).
(2)由(1)得,∠CAE=∠B=45°,AE=BD=4,
又∠BAC=45°
∴∠EAD=∠EAC+∠BAC=90°,
即△EAD是直角三角形,
∴![]()
∵AD=3
∴DE=![]() =5.
=5.


科目:初中数学 来源: 题型:
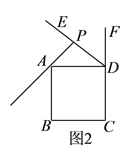
【题目】在正方形![]() 中,
中,![]() 为正方形的外角
为正方形的外角![]() 的角平分线,点
的角平分线,点![]() 在线段
在线段![]() 上,过点
上,过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,交射线
,交射线![]() 于点
于点![]() .
.
(![]() )如图1,若点
)如图1,若点![]() 与点
与点![]() 重合.
重合.
①依题意补全图1.
②判断![]() 与
与![]() 的数量关系并加以证明.
的数量关系并加以证明.
(![]() )如图2,若点
)如图2,若点![]() 恰好在线段
恰好在线段![]() 上,正方形
上,正方形![]() 的边长为
的边长为![]() ,请写出求
,请写出求![]() 长的思路(可以不写出计算结果).
长的思路(可以不写出计算结果).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,DM、EN分别垂直平分AC和BC,交AB于M、N两点,DM与EN相交于点F.
(1)若△CMN的周长为15cm,求AB的长;
(2)若∠MFN=70°,求∠MCN的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
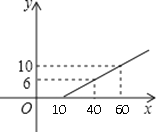
【题目】某长途汽车客运公司规定旅客可以免费携带一定质量的行李,当行李的质量超过规定时,需付的行李费y(元)与行李质量x(kg)之间的函数表达式为![]() ,这个函数的图像如图所示,求:
,这个函数的图像如图所示,求:
(1)k和b的值;
(2)旅客最多可免费携带行李的质量;
(3)行李费为4~15元时,旅客携带行李的质量为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两家快递公司揽件员(揽收快件的员工)的日工资方案如下:
甲公司为“基本工资+揽件提成”,其中基本工资为70元/日,每揽收一件提成2元;
乙公司无基本工资,仅以揽件提成计算工资.若当日揽件数不超过40,每件提成4元;若当日搅件数超过40,超过部分每件多提成2元.
如图是今年四月份甲公司揽件员人均揽件数和乙公司搅件员人均揽件数的条形统计图:

(1)现从今年四月份的30天中随机抽取1天,求这一天甲公司揽件员人均揽件数超过40(不含40)的概率;
(2)根据以上信息,以今年四月份的数据为依据,并将各公司揽件员的人均揽件数视为该公司各揽件员的
揽件数,解决以下问题:
①估计甲公司各揽件员的日平均件数;
②小明拟到甲、乙两家公司中的一家应聘揽件员,如果仅从工资收入的角度考虑,请利用所学的统计知识帮他选择,井说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,CD为AB边上的高,AD=8,CD=4,BD=3.动点P从点A出发,沿射线AB运动,速度为1个单位/秒,运动时间为t秒.
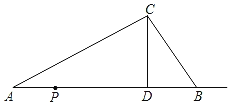
(1)当t为何值时,△PDC≌△BDC;
(2)当t为何值时,△PBC是等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠C=90°,BD平分∠ABC交AC于点D,DE垂直平分线段AB.
(1)求∠A;
(2)若DE=2cm,BD=4cm,求AC的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com