
【题目】如图,Rt△ABC中,∠ACB=90°,∠ABC=30°,AC=1,△ABC绕点C顺时针旋转一定角度得到△DEC,点D恰好落在AB边上,连接AE. 求:
(1)旋转角的度数;
(2)AE的长度.

【答案】(1)60°;(2)![]() .
.
【解析】
(1)由旋转的性质可知AC=DC, BC=EC,∠ACB=∠DCE=90°.证△ACD是等边三角形,可得∠ACD=60°,即旋转角的度数为60°;(2)连接BE,证△BCE是等边三角形.
求出BE=BC=![]() ,∠CBE=60°,由勾股定理可得:
,∠CBE=60°,由勾股定理可得:![]() .
.
(1)∵∠ACB=90°,∠ABC=30°,AC=1,
∴∠BAC=90°-∠ABC=60°,AB=2AC=2,BC=![]() .
.
由旋转的性质可知AC=DC, BC=EC,∠ACB=∠DCE=90°.
∵CA=CD,∠BAC=60°,
∴△ACD是等边三角形.
∴∠ACD=60°,即旋转角的度数为60°.
(2)连接BE,
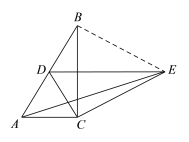
由(1),得∠BCD=30°.
∴∠BCE=60°.
∵BC=EC,
∴△BCE是等边三角形.
∴BE=BC=![]() ,∠CBE=60°.
,∠CBE=60°.
∵∠ABE=∠ABC+∠CBE=90°,
∴![]() .
.


 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:初中数学 来源: 题型:
【题目】随着地铁和共享单车的发展,“地铁![]() 单车”已成为很多市民出行的选择
单车”已成为很多市民出行的选择![]() 张老师从学校站出发,先乘坐地铁到某一站出地铁,再骑共享单车回家,设他出地铁的站点与学校距离为
张老师从学校站出发,先乘坐地铁到某一站出地铁,再骑共享单车回家,设他出地铁的站点与学校距离为![]() 单位:千米
单位:千米![]() ,乘坐地铁的时间为
,乘坐地铁的时间为![]() 单位分钟
单位分钟![]() ,经测量,得到如下数据:
,经测量,得到如下数据:
地铁站 | A | B | C | D |
| E |
| 6 |
| 10 | |
| 15 |
| 9 | 12 | a | 20 |
| b |
![]() 根据表中数据的规律,直接写出表格中a、b的值和
根据表中数据的规律,直接写出表格中a、b的值和![]() 关于x的函数表达式;
关于x的函数表达式;
![]() 张老师骑单车的时间
张老师骑单车的时间![]() 单位:分钟
单位:分钟![]() 也受x的影响,其关系可以用
也受x的影响,其关系可以用![]() 米描述,
米描述,
![]() 若张老师出地铁的站点与学校距离为14千米,请求出张老师从学校回到家所需的时间;
若张老师出地铁的站点与学校距离为14千米,请求出张老师从学校回到家所需的时间;
![]() 若张老师准备在离家较近的A,B,C,D,E中的某一站出地铁,请问:张老师应选择在哪一站出地铁,才能使他从学校回到家所需的时间最短?并求出最短时间.
若张老师准备在离家较近的A,B,C,D,E中的某一站出地铁,请问:张老师应选择在哪一站出地铁,才能使他从学校回到家所需的时间最短?并求出最短时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径的圆交AC于点D,交BC于点E,延长AE至点F,使EF=AE,连接FB,FC.
(1)求证:四边形ABFC是菱形;
(2)若AD=7,BE=2,求半圆和菱形ABFC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图在直角坐标系中,点A在y轴上,BC⊥x轴于点C,点A关于直线OB的对称点D恰好在BC上,点E与点O关于直线BC对称,∠OBC=35°,则∠OED的度数为( )
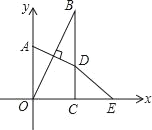
A.10°B.20°C.30°D.35°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是等边三角形ABC外接圆⊙O上的点,在以下判断中,不正确的是

A、当弦PB最长时,ΔAPC是等腰三角形 B、当ΔAPC是等腰三角形时,PO⊥AC
C、当PO⊥AC时,∠ACP=300 D、当∠ACP=300时,ΔPBC是直角三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC内接于⊙O,过点A作直线EF.
(1)如图①,AB是直径,要使EF是⊙O的切线,还须添加一个条件是(只需写出三种情况).
(ī) (īī) (īīī)
(2)如图(2),若AB为非直径的弦,∠CAE=∠B,则EF是⊙O的切线吗?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:三角形ABC中,∠A=90,AB=AC,D为BC的中点,如图,E,F分别是AB,AC上的点,且BE=AF,求证:△DEF为等腰直角三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC=12厘米,BC=9厘米,点D为AB的中点,如果点P在线段BC上以v厘米/秒的速度由B点向C点运动,同时点Q在线段CA上由C点向A点运动。若点Q的运动速度为3厘米/秒,则当△BPD与△CQP全等时,v的值为_____________
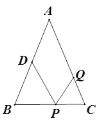
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com