
【题目】如图,在⊙O中,点C是优弧ACB的中点,D、E分别是OA、OB上的点,且AD=BE,弦CM、CN分别过点D、E.
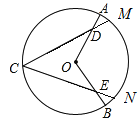
(1)求证:CD=CE.
(2)求证:![]() =
=![]() .
.
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】如图示一架水平飞行的无人机AB的尾端点A测得正前方的桥的左端点P的
俯角为α其中tanα=2![]() ,无人机的飞行高度AH为500
,无人机的飞行高度AH为500![]() 米,桥的长度为1255米.
米,桥的长度为1255米.
①求点H到桥左端点P的距离;
②若无人机前端点B测得正前方的桥的右端点Q的俯角为30°,求这架无人机的长度AB.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一儿童服装商店在销售中发现:某品牌童装平均每天可售出20件,每件盈利40元.为了迎接“六·一”儿童节,商店决定采取适当的降价措施,扩大销售量,增加盈利,尽快减少库存.经市场调查发现:如果每件童装降价1元,那么平均每天就可多售出2件.要想平均每天销售这种童装上盈利1200元,那么每件童装应降价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在小明、小红两名同学中选拔一人参加2018年张家界市“经典诗词朗诵”大赛,在相同的测试条件下,两人5次测试成绩(单位:分)如下:
小明:80,85,82,85,83 小红:88,79,90,81,72.
回答下列问题:
(1)求小明和小红测试的平均成绩;
(2)求小明和小红五次测试成绩的方差.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:△ABC的周长为30cm,把△ABC的边AC对折,使顶点C和点A重合,折痕交BC边于点D,交AC边与点E,连接AD,若AE=4cm,则△ABD的周长是( )

A. 22cmB. 20cmC. 18cmD. 15cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某企业接到一批产品的生产任务,按要求必须在14天内完成.已知每件产品的出厂价为60元.工人甲第x天生产的产品数量为y件,y与x满足如下关系:
![]()
(1)工人甲第几天生产的产品数量为70件?
(2)设第x天生产的产品成本为P元/件,P与![]() 的函数图象如图.工人甲第x天创造的利润为W元,求W与x的函数关系式,并求出第几天时利润最大,最大利润是多少?
的函数图象如图.工人甲第x天创造的利润为W元,求W与x的函数关系式,并求出第几天时利润最大,最大利润是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解题
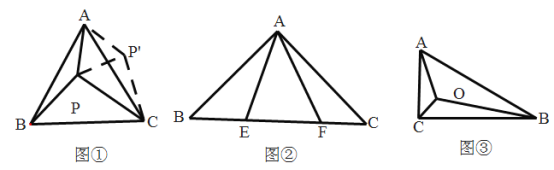
(1)阅读理解:如图①,等边![]() 内有一点
内有一点![]() ,若点
,若点![]() 到顶点
到顶点![]() ,
,![]() ,
,![]() 的距离分别为3,4,5,求
的距离分别为3,4,5,求![]() 的大小.
的大小.
思路点拨:考虑到![]() ,
,![]() ,
,![]() 不在一个三角形中,采用转化与化归的数学思想,可以将
不在一个三角形中,采用转化与化归的数学思想,可以将![]() 绕顶点
绕顶点![]() 逆时针旋转
逆时针旋转![]() 到
到![]() 处,此时
处,此时![]() ,这样,就可以利用全等三角形知识,结合已知条件,将三条线段的长度转化到一个三角形中,从而求出
,这样,就可以利用全等三角形知识,结合已知条件,将三条线段的长度转化到一个三角形中,从而求出![]() 的度数.请你写出完整的解题过程.
的度数.请你写出完整的解题过程.
(2)变式拓展:请你利用第(1)题的解答思想方法,解答下面问题:
已知如图②,![]() 中,
中,![]() ,
,![]() ,
,![]() 、
、![]() 为
为![]() 上的点且
上的点且![]() ,
,![]() ,
,![]() ,求
,求![]() 的大小.
的大小.
(3)能力提升:如图③,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 为
为![]() 内一点,连接
内一点,连接![]() ,
,![]() ,
,![]() ,且
,且![]() ,请直接写出
,请直接写出![]() 的值,即
的值,即![]() ______.
______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com