
【题目】已知关于![]() 的一元二次方程
的一元二次方程![]()
(1)若方程有实数根,求实数![]() 的取值范围;
的取值范围;
(2)若方程两实数根分别为![]() ,且满足
,且满足![]() ,求实数
,求实数![]() 的值。
的值。
【答案】(1)m≥-1;(2)m=1.
【解析】
(1)根据判别式的意义得到△=[2(m+1)]2-4(m2-1)≥0,然后解不等式即可;(2)根据根与系数的关系得到x1+x2=-(2m+1),x1x2=m2-1,再利用完全平方公式变形![]() ,得到(x1+x2)2-3x1x2-16=0,则[-2(m+1)]2-3(m2-1)-16=0,解方程得m=-9或m=1,然后利用m的取值范围确定满足条件的m的值即可.
,得到(x1+x2)2-3x1x2-16=0,则[-2(m+1)]2-3(m2-1)-16=0,解方程得m=-9或m=1,然后利用m的取值范围确定满足条件的m的值即可.
(1)由题意有△=[2(m+1)]2-4(m2-1)≥0,
整理得8m+8≥0,
解得m≥-1,
∴实数m的取值范围是m≥-1;
(2)由两根关系,得x1+x2=-(2m+1),x1x2=m2-1,
(x1-x2)2=16-x1x2,
(x1+x2)2-3x1x2-16=0,
∴[-2(m+1)]2-3(m2-1)-16=0,
∴m2+8m-9=0,
解得m=-9或m=1,
∵m≥-1,
∴m=1.


 智能训练练测考系列答案
智能训练练测考系列答案科目:初中数学 来源: 题型:
【题目】黑白两种颜色的正方形纸片,按如图所示的规律拼成若干个图案:

第4个图案中有白色纸片________块,第n个图案中有白色纸片________块。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“圆材埋壁”是我国著名的数学著作《九章算术》中的一个问题,“今有圆材,埋于壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?” 用现代的数学语言表达是:“如图,CD是⊙O的直径,弦AB⊥CD,垂足为E,CE = 1寸,AB = 1尺,求直径的长”. 依题意,CD长为( )
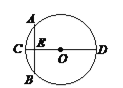
A. ![]() 寸 B. 13寸 C. 25寸 D. 26寸
寸 B. 13寸 C. 25寸 D. 26寸
查看答案和解析>>
科目:初中数学 来源: 题型:
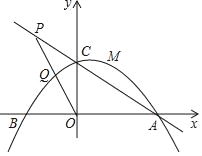
【题目】如图,抛物线y=﹣![]() (其中m>0)与x轴分别交于A,B两点(A在B的右侧),与y轴交于点c.
(其中m>0)与x轴分别交于A,B两点(A在B的右侧),与y轴交于点c.
(1)求△AOC的周长,(用含m的代数式表示)
(2)若点P为直线AC上的一点,且点P在第二象限,满足OP2=PCPA,求tan∠APO的值及用含m的代数式表示点P的坐标;
(3)在(2)的情况下,线段OP与抛物线相交于点Q,若点Q恰好为OP的中点,此时对于在抛物线上且介于点C与抛物线顶点之间(含点C与顶点)的任意一点M(x0,y0)总能使不等式n≤![]() 及不等式2n﹣
及不等式2n﹣![]() 恒成立,求n的取值范围.
恒成立,求n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
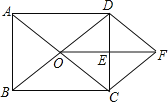
【题目】已知:如图,在矩形ABCD中,对角线AC、BD相交于点O,E是CD中点,连结OE.过点C作CF∥BD交线段OE的延长线于点F,连结DF.求证:
(1)△ODE≌△FCE;
(2)四边形ODFC是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图示一架水平飞行的无人机AB的尾端点A测得正前方的桥的左端点P的
俯角为α其中tanα=2![]() ,无人机的飞行高度AH为500
,无人机的飞行高度AH为500![]() 米,桥的长度为1255米.
米,桥的长度为1255米.
①求点H到桥左端点P的距离;
②若无人机前端点B测得正前方的桥的右端点Q的俯角为30°,求这架无人机的长度AB.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题)如图1,在Rt△ABC中,∠ACB=90°,AC=BC,过点C作直线l平行于AB.∠EDF=90°,点D在直线L上移动,角的一边DE始终经过点B,另一边DF与AC交于点P,研究DP和DB的数量关系.

(探究发现)(1)如图2,某数学兴趣小组运用从特殊到一般的数学思想,发现当点D移动到使点P与点C重合时,通过推理就可以得到DP=DB,请写出证明过程;
(数学思考)(2)如图3,若点P是AC上的任意一点(不含端点A、C),受(1)的启发,这个小组过点D作DG⊥CD交BC于点G,就可以证明DP=DB,请完成证明过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
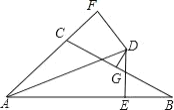
【题目】如图,△ABC 中, AB=11 , AC= 5 ,∠ BAC 的平分线 AD 与边 BC 的垂直平分线 CD 相 交于点 D ,过点 D 分别作 DE⊥AB ,DF⊥AC ,垂足分别为 E 、F ,则 BE 的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在小明、小红两名同学中选拔一人参加2018年张家界市“经典诗词朗诵”大赛,在相同的测试条件下,两人5次测试成绩(单位:分)如下:
小明:80,85,82,85,83 小红:88,79,90,81,72.
回答下列问题:
(1)求小明和小红测试的平均成绩;
(2)求小明和小红五次测试成绩的方差.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com