
【题目】(问题)如图1,在Rt△ABC中,∠ACB=90°,AC=BC,过点C作直线l平行于AB.∠EDF=90°,点D在直线L上移动,角的一边DE始终经过点B,另一边DF与AC交于点P,研究DP和DB的数量关系.

(探究发现)(1)如图2,某数学兴趣小组运用从特殊到一般的数学思想,发现当点D移动到使点P与点C重合时,通过推理就可以得到DP=DB,请写出证明过程;
(数学思考)(2)如图3,若点P是AC上的任意一点(不含端点A、C),受(1)的启发,这个小组过点D作DG⊥CD交BC于点G,就可以证明DP=DB,请完成证明过程.
【答案】(1)见解析;(2)见解析
【解析】
(1)由等腰直角三角形的性质可得∠CAB=∠CBA=45°,由平行线的性质可得∠CBA=∠DCB=45°,即可证DB=DP;(2)通过证明△CDP≌△GDB,可得DP=DB.
证明:(1)如图2
∵∠ACB=90°,AC=BC
∴∠CAB=∠CBA=45°
∵CD∥AB
∴∠CBA=∠DCB=45°,且BD⊥CD
∴∠DCB=∠DBC=45°
∴DB=DC
即DP=DB;
(2)如图3
∵DG⊥CD,∠DCB=45°
∴∠DCG=∠DGC=45°
∴DC=DG,∠DCP=∠DGB=135°,
∵∠BDP=∠CDG=90°
∴∠CDP=∠BDG
在△CDP和△GDB中,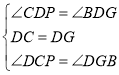
∴△CDP≌△GDB(ASA)
∴DP=DB.



 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,BD平分∠ABC交AC于G,DM∥BC交∠ABC的外角平分线于M,交AB、AC于F、E,下列结论:①MB⊥BD;②FD=FB;③MD=2CE.其中一定正确的是_____.(只填写序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把长方形纸片ABCD沿对角线折叠,设重叠部分为△EBD,那么,有下列说法:①△EBA和△EDC一定是全等三角形;②△EBD是等腰三角形,EB=ED;③折叠后得到的图形是轴对称图形;④折叠后∠ABE和∠CBD一定相等;其中正确的有( )

A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB分别与两坐标轴交于点A(4,0).B(0,8),点C的坐标为(2,0).

(1)求直线AB的解析式;
(2)在线段AB上有一动点P.
①过点P分别作x,y轴的垂线,垂足分别为点E,F,若矩形OEPF的面积为6,求点P的坐标.
②连结CP,是否存在点P,使![]() 与
与![]() 相似,若存在,求出点P的坐标,若不存在,请说明理由.
相似,若存在,求出点P的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学课上,老师提出如下问题:
尺规作图:作一个角等于已知角
已知:∠AOB,
求作:∠A′OB′,使:∠A′OB′=∠AOB

小易同学作法如下:
①作射线O′A′;
②以点O为圆心,以任意长为半径作弧,交OA于C,交OB于D;
③以点O′为圆心,以OC长为半径作弧,交O′A于C
④以点C′圆心,以CD为半径作弧,交③中所画弧于D′;
⑤经过点D′作射线O′B′,∠A′O′B′就是所求的角.

老师说:“小易的作法正确”
请回答:小易的作图依据是______________________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,EF交AB于E,交CD于F,EP平分∠AEF,FP平分∠CFE,直线MN经过点P并与AB,CD分别交于点M,N.
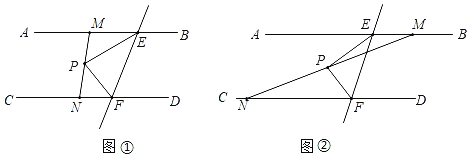
(1)如图①,求证:EM+FN=EF;
(2)如图②,(1)的结论是否成立?若成立,请证明;若不成立,直接写出EM,FN,EF三条线段的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列关于概率的说法,错误的是( )
A. 明天下雨的概率是80%,即明天80%的时间都下雨;
B. 做投掷硬币试验时,投掷的次数足够多时,正面朝上的频率就越接近于![]() ;
;
C. “13人中至少有2人生肖相同”,这是一个必然事件。
D. 连掷两枚骰子,它们的点数相同的概率是![]() ;
;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是由27个相同的小立方块搭成的几何体,它的三个视图是3×3的正方形,若拿掉若干个小立方块(几何体不倒掉),其三个视图仍都为3×3的正方形,则最多能拿掉小立方块的个数为( )

A. 10 B. 12 C. 15 D. 18
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com