
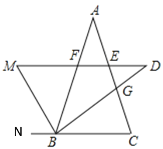
【题目】如图,△ABC中,AB=AC,BD平分∠ABC交AC于G,DM∥BC交∠ABC的外角平分线于M,交AB、AC于F、E,下列结论:①MB⊥BD;②FD=FB;③MD=2CE.其中一定正确的是_____.(只填写序号)

【答案】①②③
【解析】
根据角平分线的定义即可证出∠MBD=90°,从而证出①;根据角平分线、平行线和等腰三角形的关系即可证出②;同理可证MF=BF,根据等边对等角即可证出:∠ABC=∠ACB,然后根据平行线的性质可得:∠AFE=∠ABC,∠AEF=∠ACB,从而证出∠AFE=∠AEF,再根据等角对等边即可证出AF=AE,从而证出BF=CE,即可证出③.
解:如图,∵BD、BM分别是∠ABC及其外角的平分线,
∴∠MBD=∠MBA+∠DBA=![]() ∠NBA+
∠NBA+![]() ∠CBA=
∠CBA=![]() (∠NBA+∠CBA)=
(∠NBA+∠CBA)=![]() ∠NBC=
∠NBC=![]() ×180°=90°,
×180°=90°,
故MB⊥BD,故①成立;
∵DF∥BC,
∴∠FDB=∠DBC;
∵∠FBD=∠DBC,
∴∠FBD=∠FDB,
∴FD=BF,故②成立;
同理可证MF=BF,
∵AB=AC,
∴∠ABC=∠ACB,
∵DM∥BC,
∴∠AFE=∠ABC,∠AEF=∠ACB,
∴∠AFE=∠AEF
∴AF=AE,且AB=AC,
∴BF=CE,
∵DF=BF,MF=BF
∴MF=DF
∵∠DBM=90°,MF=DF,
∴BF=![]() DM,而CE=BF,
DM,而CE=BF,
∴CE=![]() DM,③成立.
DM,③成立.
故答案为:①②③.


 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:
【题目】(9分)如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(-3,2),B(0,4),C(0,2).
(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C;平移△ABC,若A的对应点A2的坐标为(0,4),画出平移后对应的△A2B2C2;
(2)若将△A1B1C绕某一点旋转可以得到△A2B2C2,请直接写出旋转中心的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
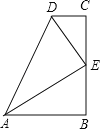
【题目】如图,∠B=∠C=90°,E是BC的中点,DE平分∠ADC.
(1)求证:AE平分∠DAB;
(2)若AD=8,BC=6,求四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】黑白两种颜色的正方形纸片,按如图所示的规律拼成若干个图案:

第4个图案中有白色纸片________块,第n个图案中有白色纸片________块。
查看答案和解析>>
科目:初中数学 来源: 题型:
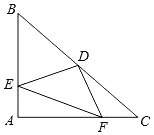
【题目】如图,△ABC是等腰直角三角形,AB=AC,D是斜边BC的中点,E.F分别是AB、AC边上的点,且DE⊥DF,
(1)求证:CF=AE;
(2)若BE=8,CF=6,求线段EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD⊥BC,BE⊥AC,垂足分别为点D、E,AD与BE交于点F,BF=AC, ∠ABE=22°,则∠CAD的度数是________°.

查看答案和解析>>
科目:初中数学 来源: 题型:
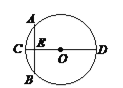
【题目】“圆材埋壁”是我国著名的数学著作《九章算术》中的一个问题,“今有圆材,埋于壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?” 用现代的数学语言表达是:“如图,CD是⊙O的直径,弦AB⊥CD,垂足为E,CE = 1寸,AB = 1尺,求直径的长”. 依题意,CD长为( )
A. ![]() 寸 B. 13寸 C. 25寸 D. 26寸
寸 B. 13寸 C. 25寸 D. 26寸
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题)如图1,在Rt△ABC中,∠ACB=90°,AC=BC,过点C作直线l平行于AB.∠EDF=90°,点D在直线L上移动,角的一边DE始终经过点B,另一边DF与AC交于点P,研究DP和DB的数量关系.

(探究发现)(1)如图2,某数学兴趣小组运用从特殊到一般的数学思想,发现当点D移动到使点P与点C重合时,通过推理就可以得到DP=DB,请写出证明过程;
(数学思考)(2)如图3,若点P是AC上的任意一点(不含端点A、C),受(1)的启发,这个小组过点D作DG⊥CD交BC于点G,就可以证明DP=DB,请完成证明过程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com