
【题目】如图,将正方形OABC放在平面直角坐标系中,O是原点,A的坐标为(1,2),则点C的坐标为_____.
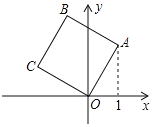
【答案】(﹣2,1).
【解析】
过点A作AD⊥x轴于D,过点C作CE⊥x轴于E,根据正方形的性质和同角的余角相等证出:OA=OC,∠OAD=∠COE,然后利用AAS即可证出△AOD≌△OCE,从而得出OE=AD=2,CE=OD=1,再结合C点所在象限即可求出C点坐标.
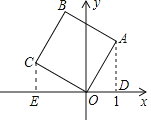
解:过点A作AD⊥x轴于D,过点C作CE⊥x轴于E, 如图所示
∵四边形OABC是正方形,
∴OA=OC,∠AOC=90°,
∴∠COE+∠AOD=90°,
又∵∠OAD+∠AOD=90°,
∴∠OAD=∠COE,
在△AOD和△OCE中,
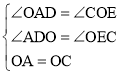 ,
,
∴△AOD≌△OCE(AAS),
∴OE=AD=2,CE=OD=1,
∵点C在第二象限,
∴点C的坐标为(﹣2,1).
故答案为(﹣2,1).


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:
【题目】如图,![]() 是
是![]() 的直径,
的直径,![]() 是半圆
是半圆![]() 上的一点,
上的一点,![]() 平分
平分![]() ,
,![]() ,垂足为
,垂足为![]() ,
,![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .
.
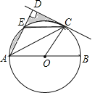
![]() 判断
判断![]() 与
与![]() 的位置关系,并证明你的结论;
的位置关系,并证明你的结论;
![]() 若
若![]() 是
是![]() 的中点,
的中点,![]() 的半径为
的半径为![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ACB中,∠ACB=90°,△ABC的角平分线AD、BE相交于点P,过P作PF⊥AD交BC的延长线于点F,交AC于点H,则下列结论:①∠APB=135°;②PF=PA;③AH+BD=AB;④S四边形ABDE=![]() S△ABP,其中正确的是( )
S△ABP,其中正确的是( )

A.①③B.①②④C.①②③D.②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上一点,点E在BC边上,连结AE、DE、DC,且AE=CD.

(1)求证:△ABE≌△CBD;
(2)若∠CAE=30°,求∠BDC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,BD平分∠ABC交AC于G,DM∥BC交∠ABC的外角平分线于M,交AB、AC于F、E,下列结论:①MB⊥BD;②FD=FB;③MD=2CE.其中一定正确的是_____.(只填写序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】模型发现:
同学们知道,三角形的两边之和大于第三边,即如图1,在△ABC中,AB+AC>BC.对于图1,若把点C看作是线段AB外一动点,且AB=c,AC=b,则线段BC的长会因为点C的位置的不同而发生变化.
因为AB、AC的长度固定,所以当∠BAC越大时,BC边越长.
特别的,当点C位于 时,线段BC的长取得最大值,且最大值为 (用含b,c的式子表示)(直接填空)
模型应用:
点C为线段AB外一动点,且AB=3,AC=2,如图2所示,分别以AC,BC为边,作等边三角形ACD和等边三角形BCE,连接BD,AE.
(1)求证:BD=AE.
(2)线段AE长的最大值为 .
模型拓展:
如图3,在平面直角坐标系中,点A是y轴正半轴上的一动点,点B是x轴正半轴上的一动点,且AB=8.若AC⊥AB,AC=3,试求OC长的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】课题学习:设计概率模拟实验.
在学习概率时,老师说:“掷一枚质地均匀的硬币,大量重复实验后,正面朝上的概率约是![]() .”小海、小东、小英分别设计了下列三个模拟实验:
.”小海、小东、小英分别设计了下列三个模拟实验:
小海找来一个啤酒瓶盖(如图1)进行大量重复抛掷,然后计算瓶盖口朝上的次数与总次数的比值;
小东用硬纸片做了一个圆形转盘,转盘上分成8个大小一样的扇形区域,并依次标上1至8个数字(如图2),转动转盘10次,然后计算指针落在奇数区域的次数与总次数的比值;
小英在一个不透明的盒子里放了四枚除颜色外都相同的围棋子(如图3),其中有三枚是白子,一枚是黑子,从中随机同时摸出两枚棋子,并大量重复上述实验,然后计算摸出的两枚棋子颜色不同的次数与总次数的比值.

根据以上材料回答问题:
小海、小东、小英三人中,哪一位同学的实验设计比较合理,并简要说出其他两位同学实验的不足之处.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB分别与两坐标轴交于点A(4,0).B(0,8),点C的坐标为(2,0).

(1)求直线AB的解析式;
(2)在线段AB上有一动点P.
①过点P分别作x,y轴的垂线,垂足分别为点E,F,若矩形OEPF的面积为6,求点P的坐标.
②连结CP,是否存在点P,使![]() 与
与![]() 相似,若存在,求出点P的坐标,若不存在,请说明理由.
相似,若存在,求出点P的坐标,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com