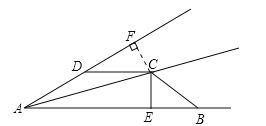
【题目】四边形ABCD中，AC平分∠BAD，CE⊥AB于E，∠ADC+∠CBE=180°，求证：2AE=AB+AD.
【答案】见解析
【解析】
过C作CF⊥AD于F，由条件可证△AFC≌△AEC，得到CF=CE．再由条件∠ADC+∠CBE=180°，证△CDF≌△CEB，由全等的性质可得DF=EB，再由线段和差可得.
证明：过C作CF⊥AD于F，
∵AC平分∠BAD，
∴∠FAC=∠EAC，
∵CE⊥AB，CF⊥AD，
∴∠DFC=∠CEB=∠CEA=90°，
∵AC=AC
∴△AFC≌△AEC，
∴AF=AE，CF=CE，
∵∠ADC+∠CBE=180°，∠ADC+∠FDC=180°
∴∠FDC=∠CBE，
∴△FDC≌△EBC，
∴DF=EB，
∴AB+AD=AE+EB+AD=AE+DF+AD=AF+AE=2AE，
∴2AE=AB+AD.
全优冲刺100分系列答案
英才点津系列答案科目：初中数学 来源： 题型：
【题目】某水果批发商销售每箱进价为40元的苹果，物价部门规定每箱售价不得高于55元，市场调查发现，若每箱以50元的价格调查，平均每天销售90箱，价格每提高1元，平均每天少销售3箱．
（1）求平均每天销售量y（箱）与销售价x（元/箱）之间的函数关系式．
（2）求该批发商平均每天的销售利润w（元）与销售价x（元/箱）之间的函数关系式．
（3）当每箱苹果的销售价为多少元时，可以获得最大利润？最大利润是多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知△ABC中，∠ABC=90°，AB=BC，AE是∠BAC的角平分线.CD⊥AE，与AE的延长线交于D点，与AB的延长线交于F点。求证CD=
AE
查看答案和解析>>
科目：初中数学 来源： 题型：
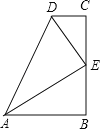
【题目】如图，∠B＝∠C＝90°，E是BC的中点，DE平分∠ADC．
（1）求证：AE平分∠DAB；
（2）若AD＝8，BC＝6，求四边形ABCD的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
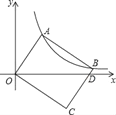
【题目】如图，在直角坐标系中，矩形OABC的顶点A、B在双曲线y=
（ x＞0）上，BC与x轴交于点D．若点A的坐标为（1，2），则点B的坐标为（ ）
A. （3，
） B. （4，
） C. （
，
） D. （5，
）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】黑白两种颜色的正方形纸片，按如图所示的规律拼成若干个图案：
第4个图案中有白色纸片________块，第n个图案中有白色纸片________块。
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，AD⊥BC，BE⊥AC，垂足分别为点D、E，AD与BE交于点F，BF=AC， ∠ABE=22°，则∠CAD的度数是________°.
查看答案和解析>>
科目：初中数学 来源： 题型：
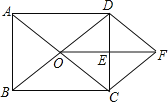
【题目】已知：如图，在矩形ABCD中，对角线AC、BD相交于点O，E是CD中点，连结OE．过点C作CF∥BD交线段OE的延长线于点F，连结DF．求证：
（1）△ODE≌△FCE；
（2）四边形ODFC是菱形．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
