
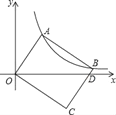
【题目】如图,在直角坐标系中,矩形OABC的顶点A、B在双曲线y=![]() ( x>0)上,BC与x轴交于点D.若点A的坐标为(1,2),则点B的坐标为( )
( x>0)上,BC与x轴交于点D.若点A的坐标为(1,2),则点B的坐标为( )
A. (3,![]() ) B. (4,
) B. (4,![]() ) C. (
) C. (![]() ,
,![]() ) D. (5,
) D. (5,![]() )
)
【答案】B
【解析】
由矩形OABC的顶点A、B在双曲线y=![]() (x>0)上,BC与x轴交于点D.若点A的坐标为(1,2),利用待定系数法即可求得反比例函数与直线OA的解析式,又由OA⊥AB,可得直线AB的系数为:
(x>0)上,BC与x轴交于点D.若点A的坐标为(1,2),利用待定系数法即可求得反比例函数与直线OA的解析式,又由OA⊥AB,可得直线AB的系数为:![]() ,继而可求得直线AB的解析式,将直线AB与反比例函数联立,即可求得点B的坐标.
,继而可求得直线AB的解析式,将直线AB与反比例函数联立,即可求得点B的坐标.
∵矩形OABC的顶点A. B在双曲线y=![]() (x>0)上,点A的坐标为(1,2),
(x>0)上,点A的坐标为(1,2),
∴2=![]() ,
,
解得:k=2,
∴双曲线的解析式为:y=![]() ,直线OA的解析式为:y=2x,
,直线OA的解析式为:y=2x,
∵OA⊥AB,
∴设直线AB的解析式为:y=![]() x+b,
x+b,
∴2=![]() ×1+b,
×1+b,
解得:b=![]() ,
,
∴直线AB的解析式为:y=![]() x+
x+![]() ,
,
将直线AB与反比例函数联立得出:
y=![]() y=
y=![]() x+
x+![]() ,
,
解得:x=4,y=![]() 或x=1,y=2,
或x=1,y=2,
∴点B(4,![]() ).
).
故选B.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】已知:AB⊥AC,DE⊥AB,AC=BE,BC=BD,

(1)求证:BC⊥BD;
(2)若点F是BC,BD的垂直平分线的交点,连接FA、FE.填空:判断△AFE的形状是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了迎接省一级示范学校的验收,广安二中决定对学校校园内的环校跑道进行改造,需要铺设一条长为4200米的道路,根据招标文件得知甲工程队比乙工程队每天能多铺设20米.甲工程队铺设350米所用的天数与乙工程队铺设250米所用的天数相同.
![]() 甲、乙工程队每天各能铺设多少米?
甲、乙工程队每天各能铺设多少米?
![]() 施工时,需付给甲队每天施工费3000元,需付给乙队每天施工费2500元,单独承包给甲队或乙队,或者两队一起施工都可以,但为了节约经费,方便全校师生出行,聪明的同学们你认为三种承包方式怎样承包最合理?
施工时,需付给甲队每天施工费3000元,需付给乙队每天施工费2500元,单独承包给甲队或乙队,或者两队一起施工都可以,但为了节约经费,方便全校师生出行,聪明的同学们你认为三种承包方式怎样承包最合理?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ACB中,∠ACB=90°,△ABC的角平分线AD、BE相交于点P,过P作PF⊥AD交BC的延长线于点F,交AC于点H,则下列结论:①∠APB=135°;②PF=PA;③AH+BD=AB;④S四边形ABDE=![]() S△ABP,其中正确的是( )
S△ABP,其中正确的是( )

A.①③B.①②④C.①②③D.②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把一枚六个面编号为1,2,3,4,5,6的质地均匀的正六面体骰子连续投掷2次,若两次正面朝上的编号分别为m、n,则二次函数y=x2+mx+2n的图象与x轴至少有一个交点的概率是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上一点,点E在BC边上,连结AE、DE、DC,且AE=CD.

(1)求证:△ABE≌△CBD;
(2)若∠CAE=30°,求∠BDC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】模型发现:
同学们知道,三角形的两边之和大于第三边,即如图1,在△ABC中,AB+AC>BC.对于图1,若把点C看作是线段AB外一动点,且AB=c,AC=b,则线段BC的长会因为点C的位置的不同而发生变化.
因为AB、AC的长度固定,所以当∠BAC越大时,BC边越长.
特别的,当点C位于 时,线段BC的长取得最大值,且最大值为 (用含b,c的式子表示)(直接填空)
模型应用:
点C为线段AB外一动点,且AB=3,AC=2,如图2所示,分别以AC,BC为边,作等边三角形ACD和等边三角形BCE,连接BD,AE.
(1)求证:BD=AE.
(2)线段AE长的最大值为 .
模型拓展:
如图3,在平面直角坐标系中,点A是y轴正半轴上的一动点,点B是x轴正半轴上的一动点,且AB=8.若AC⊥AB,AC=3,试求OC长的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,∠ABC和∠BCD的平分线交于AD边上一点E,且BE=4,CE=3,则AB的长是( )

A. ![]() B. 3 C. 4 D. 5
B. 3 C. 4 D. 5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com