
【题目】如图,∠B=∠C=90°,E是BC的中点,DE平分∠ADC.
(1)求证:AE平分∠DAB;
(2)若AD=8,BC=6,求四边形ABCD的面积.
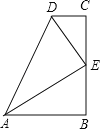
【答案】(1)证明见解析;(2)24.
【解析】
(1)过点E作EF⊥DA于点F,首先根据角的平分线上的点到角的两边的距离相等可得CE=EF,根据等量代换可得BE=EF,再根据角平分线的判定可得AE平分∠BAD;
(2)根据角平分线的性质可得CD=DF,AB=AF,可求CD+AB,再利用梯形的面积公式可得答案.
(1)过点E作EF⊥DA于点F,
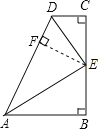
∵∠C=90°,DE平分∠ADC,
∴CE=EF,
∵E是BC的中点,
∴BE=CE,
∴BE=EF,
又∵∠B=90°,EF⊥AD,
∴AE平分∠DAB.
(2)∵∠C=90°,DE平分∠ADC,EF⊥DA,
∴CD=DF,
∵∠B=90°,AE是∠DAB的平分线,
∴AB=AF,
∴CD+AB=DF+AF=AD=8,
∴S梯形ABCD=8×6÷2=24.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】解决下列两个问题:
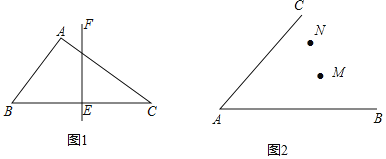
(1)如图1,在△ABC中,AB=4,AC=6,BC=7,EF垂直平分BC,P为直线EF上一动点,PA+PB的最小值为______,并在图中标出当PA+PB取最小值时点P的位置.
(2)如图2,点M、N在∠BAC的内部,请在∠BAC的内部求作一点P,使得点P到∠BAC两边的距离相等,且使PM=PN.(尺规作图,保留作图痕迹,无需证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
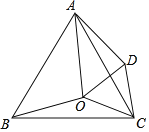
【题目】如图,O在等边△ABC内,∠BOC=150°,将△BOC绕点C顺时针旋转后,得△ADC,连接OD.
(1)△COD是______三角形.
(2)若OB=5,OC=3,求OA的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】圆桌面(桌面中间有一个直径为0.4m的圆洞)正上方的灯泡(看作一个点)发出的光线照射平行于地面的桌面后,在地面上形成如图所示的圆环形阴影.已知桌面直径为1.2m,桌面离地面1m,若灯泡离地面3m,则地面圆环形阴影的面积是( )

A. 0.324πm2 B. 0.288πm2 C. 1.08πm2 D. 0.72πm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ACB中,∠ACB=90°,△ABC的角平分线AD、BE相交于点P,过P作PF⊥AD交BC的延长线于点F,交AC于点H,则下列结论:①∠APB=135°;②PF=PA;③AH+BD=AB;④S四边形ABDE=![]() S△ABP,其中正确的是( )
S△ABP,其中正确的是( )

A.①③B.①②④C.①②③D.②③
查看答案和解析>>
科目:初中数学 来源: 题型:
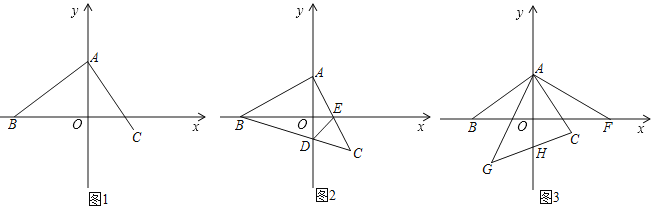
【题目】如图,点A(0,2)在y轴上,点B在x轴上,作∠BAC=90°,并使AB=AC.
(1)如图1,若点B的坐标为(﹣3,0),求点C的坐标.
(2)如图2,若点B的坐标为(﹣4,0),连接BC交y轴于点D,AC交x轴于点E,连接DE,求证:BE=AD+DE.
(3)在(1)的条件下,如图3,F为(4,0),作∠FAG=90°,并使AF=AG,连接GC交y轴于点H,求点H的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,BD平分∠ABC交AC于G,DM∥BC交∠ABC的外角平分线于M,交AB、AC于F、E,下列结论:①MB⊥BD;②FD=FB;③MD=2CE.其中一定正确的是_____.(只填写序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把长方形纸片ABCD沿对角线折叠,设重叠部分为△EBD,那么,有下列说法:①△EBA和△EDC一定是全等三角形;②△EBD是等腰三角形,EB=ED;③折叠后得到的图形是轴对称图形;④折叠后∠ABE和∠CBD一定相等;其中正确的有( )

A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com