
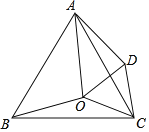
【题目】如图,O在等边△ABC内,∠BOC=150°,将△BOC绕点C顺时针旋转后,得△ADC,连接OD.
(1)△COD是______三角形.
(2)若OB=5,OC=3,求OA的长.
【答案】(1)等边;(2)OA=![]() .
.
【解析】
(1)由旋转的性质可得CO=CD,AD=BO,∠ACB=∠DCO=60°,可证△COD是等边三角形;
(2)由等边三角形的性质可得OD=OC=3,∠CDO=60°,可得∠ADO=90°,由勾股定理可求OA的长.
解:(1)∵将△BOC绕点C顺时针旋转后,得△ADC,
∴△BOC≌△ADC,
∴CO=CD,AD=BO=5,∠ACB=∠DCO=60°,
∴△COD是等边三角形,
故答案为:等边;
(2)∵△COD是等边三角形,
∴OD=OC=3,∠CDO=60°,
∵△BOC≌△ADC,
∴∠ADC =∠BOC=150°,
∴∠ADO=∠ADC﹣∠ODC=90°,
∴AO2=AD2+OD2=9+25=34,
∴AO=![]() .
.


科目:初中数学 来源: 题型:
【题目】某水果批发商销售每箱进价为40元的苹果,物价部门规定每箱售价不得高于55元,市场调查发现,若每箱以50元的价格调查,平均每天销售90箱,价格每提高1元,平均每天少销售3箱.
(1)求平均每天销售量y(箱)与销售价x(元/箱)之间的函数关系式.
(2)求该批发商平均每天的销售利润w(元)与销售价x(元/箱)之间的函数关系式.
(3)当每箱苹果的销售价为多少元时,可以获得最大利润?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(9分)如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(-3,2),B(0,4),C(0,2).
(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C;平移△ABC,若A的对应点A2的坐标为(0,4),画出平移后对应的△A2B2C2;
(2)若将△A1B1C绕某一点旋转可以得到△A2B2C2,请直接写出旋转中心的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
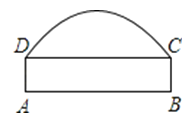
【题目】如图,有一条双向公路隧道,其横断面由抛物线和矩形ABCD的三边DA、AB、BC围成,隧道最大高度为4.9米,AB=10米,BC=2.4米,若有一辆高为4米、宽为2米的集装箱的汽车要通过隧道,为了使箱顶不碰到隧道顶部,又不违反交通规则(汽车应靠道路右侧行驶,不能超过道路中线),汽车的右侧必须离开隧道右壁几米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图所示,给出以下结论:①a+b+c<0;②b2-4ac>0;③b>0;④4a-2b+c<0;⑤c-a>1,其中正确的结论有( )
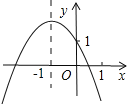
A. ①②④ B. ①②③ C. ①②⑤ D. ①②④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,∠ABC=90°,AB=BC,AE是∠BAC的角平分线.CD⊥AE,与AE的延长线交于D点,与AB的延长线交于F点。求证CD=![]() AE
AE

查看答案和解析>>
科目:初中数学 来源: 题型:
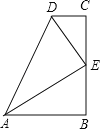
【题目】如图,∠B=∠C=90°,E是BC的中点,DE平分∠ADC.
(1)求证:AE平分∠DAB;
(2)若AD=8,BC=6,求四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD⊥BC,BE⊥AC,垂足分别为点D、E,AD与BE交于点F,BF=AC, ∠ABE=22°,则∠CAD的度数是________°.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com