
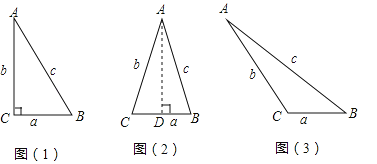
【题目】在△ABC中,BC=a,AC=b,AB=c,若∠C=90°,如图1,则有![]() ;若△ABC为锐角三角形时,小明猜想:
;若△ABC为锐角三角形时,小明猜想:![]() ,理由如下:如图2,过点A作AD⊥CB于点D,设CD=x.在Rt△ADC中,
,理由如下:如图2,过点A作AD⊥CB于点D,设CD=x.在Rt△ADC中,![]() ,在Rt△ADB中,
,在Rt△ADB中,![]() ,∴
,∴![]() .
.
∵a>0,x>0,∴2ax>0,∴![]() ,∴当△ABC为锐角三角形时
,∴当△ABC为锐角三角形时![]() .
.
所以小明的猜想是正确的.
(1)请你猜想,当△ABC为钝角三角形时, ![]() 与
与![]() 的大小关系.
的大小关系.
(2)温馨提示:在图3中,作BC边上的高.
(3)证明你猜想的结论是否正确.
科目:初中数学 来源: 题型:
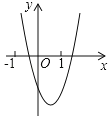
【题目】抛物线y=ax2+bx+c的图象如图所示,那么一次函数y=bx+b2﹣4ac与反比例函数y=![]() 在同一坐标系内的图象大致是( )
在同一坐标系内的图象大致是( )
A.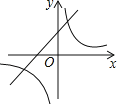 B.
B.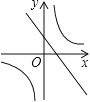
C.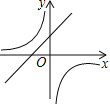 D.
D.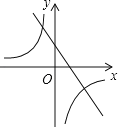
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,抛物线y=﹣![]() x2+
x2+![]() x+
x+![]() 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,对称轴与x轴交于点D.
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,对称轴与x轴交于点D.
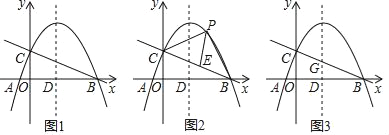
(1)求直线BC的解析式;
(2)如图2,点P为直线BC上方抛物线上一点,连接PB、PC.当△PBC的面积最大时,在线段BC上找一点E(不与B、C重合),使PE+![]() BE的值最小,求点P的坐标和PE+
BE的值最小,求点P的坐标和PE+![]() BE的最小值;
BE的最小值;
(3)如图3,点G是线段CB的中点,将抛物线y=﹣![]() x2+
x2+![]() x+
x+![]() 沿x轴正方向平移得到新抛物线y′,y′经过点D,y′的顶点为F.在抛物线y′的对称轴上,是否存在一点Q,使得△FGQ为直角三角形?若存在,直接写出点Q的坐标;若不存在,请说明理由.
沿x轴正方向平移得到新抛物线y′,y′经过点D,y′的顶点为F.在抛物线y′的对称轴上,是否存在一点Q,使得△FGQ为直角三角形?若存在,直接写出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,AB=AC,CD是∠ACB的平分线,DE∥BC,交AC于点 E.
(1)求证:DE=CE.
(2)若∠CDE=35°,求∠A 的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个工程队共同参与一项筑路工程,甲队单独施工3个月,这时增加了乙队,两队又共同工作了2个月,总工程全部完成,已知甲队单独完成全部工程比乙队单独完成全部工程多用2个月,设甲队单独完成全部工程需![]() 个月,则根据题意可列方程中错误的是( )
个月,则根据题意可列方程中错误的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
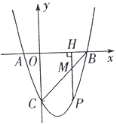
【题目】如图,二次函数y=ax2+bx-3的图象与x轴相交于A(-1,0),B(3,0)两点.与y轴相交于点C
(1)求这个二次函数的解析式.
(2)若P是第四象限内这个二次函数的图象上任意一点,PH⊥x轴于点H,与BC交于点M,请问:当点P的坐标为多少时,线段PM的长最大?并求出这个最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com