
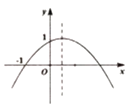
【题目】如图,二次函数![]() 的图象的顶点在第一象限,且过点
的图象的顶点在第一象限,且过点![]() 和
和![]() ,以下结论:①
,以下结论:①![]() ,②
,②![]() ,③
,③![]() ,④当
,④当![]() 时,
时,![]() .其中正确的结论的个数是( )
.其中正确的结论的个数是( )
A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
【答案】C
【解析】
由抛物线开口方向得a<0,利用对称轴在y轴的右侧得b>0,则可对①进行判断;根据二次函数图象上点的坐标特征得c=1,a-b+c=0,则b=a+c=a+1,可得0<b<1,于是可对②进行判断;由于a+b+c=a+a+1+1=2a+2,利用a<0可得a+b+c<2,再根据抛物线的对称性得到抛物线与x轴的另一个交点在(1,0)的右侧,则x=1时,函数值为正数,即a+b+c>0,由此可对③进行判断;观察函数图象得到x>-1时,抛物线有部分在x轴上方,有部分在x轴下方,则可对④进行判断.
∵由抛物线开口向下,
∴a<0,
∵对称轴在y轴的右侧,
∴b>0,
∴ab<0,故①正确;
∵点(0,1)和(1,0)都在抛物线y=ax2+bx+c上,
∴c=1,ab+c=0,
∴b=a+c=a+1,
又∵a<0,
∴0<b<1,故②正确;
∵a+b+c=a+a+1+1=2a+2,
又∵a<0,
∴2a+2<2,即a+b+c<2,
∵抛物线与x轴的一个交点坐标为(1,0),抛物线的对称轴在y轴右侧,
∴抛物线与x轴的另一个交点在点(1,0)的右侧,
又∵抛物线开口向下,
∴x=1时,y>0,即a+b+c>0,
∴0<a+b+c<2,故③正确;
∵x>1时,抛物线有部分在x轴上方,有部分在x轴下方,
∴y>0或y=0或y<0,故④错误.
故选:C.


 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:初中数学 来源: 题型:
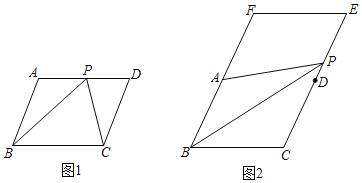
【题目】请分别在下列图中使用无刻度的直尺按要求画图.
(1)在图1中,点P是ABCD边AD上的中点,过点P画一条线段PM,使PM=![]() AB.
AB.
(2)在图2中,点A、D分别是BCEF边FB和EC上的中点,且点P是边EC上的动点,画出△PAB的一条中位线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋中装有![]() 个分别标有数
个分别标有数![]() 的小球,它们的形状、大小完全相同,小红先从口袋里随机摸出一个小球记下数为
的小球,它们的形状、大小完全相同,小红先从口袋里随机摸出一个小球记下数为![]() ,小颖在剩下的
,小颖在剩下的![]() 个球中随机摸出一个小球记下数为
个球中随机摸出一个小球记下数为![]() ,这样确定了点
,这样确定了点![]() 的坐标.
的坐标.![]()
(1)请你利用列表法或画树状图法求点![]() 的横、纵坐标均能被
的横、纵坐标均能被![]() 整除的概率.
整除的概率.
(2)记点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,求点
,求点![]() 位于反比例函数
位于反比例函数![]() 图象上的概率.
图象上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=x2+bx+c的对称轴为直线x=1,且经过点(﹣1,0).若关于x的一元二次方程x2+bx+c﹣t=0(t为实数)在﹣1<x<4的范围内有实数根,则t的取值范围是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A(3,4),点B为直线x=﹣2上的动点,点C(x,0)且﹣2<x<3,BC⊥AC垂足为点C,连接AB.若AB与y轴正半轴的所夹锐角为α,当tanα的值最大时x的值为( )

A.![]() B.
B.![]() C.1D.
C.1D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
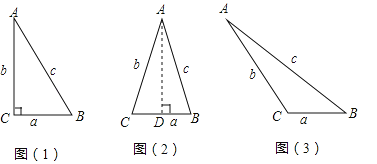
【题目】在△ABC中,BC=a,AC=b,AB=c,若∠C=90°,如图1,则有![]() ;若△ABC为锐角三角形时,小明猜想:
;若△ABC为锐角三角形时,小明猜想:![]() ,理由如下:如图2,过点A作AD⊥CB于点D,设CD=x.在Rt△ADC中,
,理由如下:如图2,过点A作AD⊥CB于点D,设CD=x.在Rt△ADC中,![]() ,在Rt△ADB中,
,在Rt△ADB中,![]() ,∴
,∴![]() .
.
∵a>0,x>0,∴2ax>0,∴![]() ,∴当△ABC为锐角三角形时
,∴当△ABC为锐角三角形时![]() .
.
所以小明的猜想是正确的.
(1)请你猜想,当△ABC为钝角三角形时, ![]() 与
与![]() 的大小关系.
的大小关系.
(2)温馨提示:在图3中,作BC边上的高.
(3)证明你猜想的结论是否正确.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com