
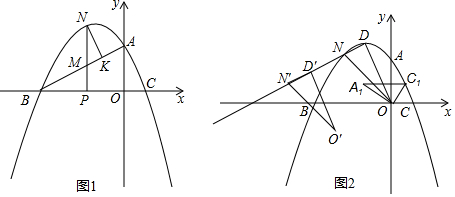
分析 (1)利用待定系数法以及顶点坐标公式即可解决问题.
(2)如图1中,设P(m,0)则N(m,=-$\frac{\sqrt{3}}{3}$m2-$\frac{2}{3}$$\sqrt{3}$m+$\sqrt{3}$).由△NMK∽△BMN,又△MNK与△MPB的面积相等,推出△NMK≌△BMN,推出MN=BM,在Rt△ABO中,tan∠ABO=$\frac{AO}{OB}$=$\frac{\sqrt{3}}{3}$,推出∠ABO=30°,推出BM=2PM=MN,可得-$\frac{\sqrt{3}}{3}$m2-$\frac{2}{3}$$\sqrt{3}$m+$\sqrt{3}$-$\frac{\sqrt{3}}{3}$m+$\sqrt{3}$=2($\frac{\sqrt{3}}{3}$m+$\sqrt{3}$),解得m=-2或-3(舍弃),推出N(-2,$\sqrt{3}$),
在y轴上取一点F,使得∠OCF=30°,作QH⊥CF于H,因为QH=$\frac{1}{2}$CQ,所以NQ+$\frac{1}{2}$CQ=NQ+QH,根据垂线段最短可知,当N、Q、H共线,且NH⊥CF时,NQ+$\frac{1}{2}$CQ=NQ+QH的值最小.由此即可解决问题.
(3)首先求出点A′的坐标,再证明A′N⊥DN,分三种情形讨论即可.①如图3中,当A′D′=A′N′时.②如图4中,当N′D′=N′A′时.③如图5中,延长C′A′交DG于N′,此时△D′N′A′是等腰三角形.
解答 解:(1)把B(-3,0),A(0,$\sqrt{3}$)的坐标代入y=-$\frac{\sqrt{3}}{3}$x2+bx+c,得到$\left\{\begin{array}{l}{-3\sqrt{3}-3b+c=0}\\{c=\sqrt{3}}\end{array}\right.$,
解得$\left\{\begin{array}{l}{b=-\frac{2}{3}\sqrt{3}}\\{c=\sqrt{3}}\end{array}\right.$,
∴二次函数的解析式为y=-$\frac{\sqrt{3}}{3}$x2-$\frac{2}{3}$$\sqrt{3}$x+$\sqrt{3}$,
顶点D的坐标为(-1,$\frac{4}{3}$$\sqrt{3}$).
(2)如图1中,设P(m,0)则N(m,=-$\frac{\sqrt{3}}{3}$m2-$\frac{2}{3}$$\sqrt{3}$m+$\sqrt{3}$).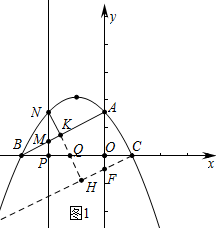
∵A(0,$\sqrt{3}$),B(-3,0),
∴直线AB的解析式为y=$\frac{\sqrt{3}}{3}$x+$\sqrt{3}$,AB用PN的交点M(m,$\frac{\sqrt{3}}{3}$m+$\sqrt{3}$),
∵∠NMK=∠BMP,∠NKM=∠MPB=90°,
∴△NMK∽△BMN,
∵△MNK与△MPB的面积相等,
∴△NMK≌△BMN,
∴MN=BM,
在Rt△ABO中,tan∠ABO=$\frac{AO}{OB}$=$\frac{\sqrt{3}}{3}$,
∴∠ABO=30°,
∴BM=2PM=MN,
∴-$\frac{\sqrt{3}}{3}$m2-$\frac{2}{3}$$\sqrt{3}$m+$\sqrt{3}$-$\frac{\sqrt{3}}{3}$m+$\sqrt{3}$=2($\frac{\sqrt{3}}{3}$m+$\sqrt{3}$),
解得m=-2或-3(舍弃),
∴N(-2,$\sqrt{3}$),
在y轴上取一点F,使得∠OCF=30°,作QH⊥CF于H,
∵QH=$\frac{1}{2}$CQ,
∴NQ+$\frac{1}{2}$CQ=NQ+QH,
根据垂线段最短可知,当N、Q、H共线,且NH⊥CF时,NQ+$\frac{1}{2}$CQ=NQ+QH的值最小.
∵直线CF的解析式为y=$\frac{\sqrt{3}}{3}$x-$\frac{\sqrt{3}}{3}$,直线NH的解析式为y=-$\sqrt{3}$x-$\sqrt{3}$,
∴Q(-1,0),
由$\left\{\begin{array}{l}{y=-\sqrt{3}x-\sqrt{3}}\\{y=\frac{\sqrt{3}}{3}x-\frac{\sqrt{3}}{3}}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=-\frac{1}{2}}\\{y=-\frac{\sqrt{3}}{2}}\end{array}\right.$,
∴H(-$\frac{1}{2}$,-$\frac{\sqrt{3}}{2}$),
∴NH=$\sqrt{(2-\frac{1}{2})^{2}+(\sqrt{3}+\frac{\sqrt{3}}{2})^{2}}$=3,
∴NQ+$\frac{1}{2}$CQ=NQ+QH的最小值为3.
(3)如图2中,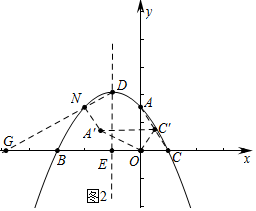
在Rt△AOC中,∵OA=$\sqrt{3}$,OC=1,AC=2,
∴tan∠ACO=$\sqrt{3}$,
∴∠ACO=60°,
∵OC′=OC,
∴△COC′是等边三角形,
∴∠A′C′C=∠C′OC=60°,
∴A′C′∥OC,
∴A′(-$\frac{3}{2}$,$\frac{\sqrt{3}}{2}$),
∵N(-2,$\sqrt{3}$),D(-1,$\frac{4}{3}$$\sqrt{3}$),
∴直线DN的解析式为y=$\frac{\sqrt{3}}{3}$x+$\frac{5}{3}$$\sqrt{3}$,直线AN的解析式y=-$\sqrt{3}$x-$\sqrt{3}$,
∵$\frac{\sqrt{3}}{3}$×(-$\sqrt{3}$)=-1,
∴AN⊥DN,设直线DN交x轴于G,则G(-5,0),对称轴与x轴的交点为E(-1,0),
在Rt△DGE中,tan∠DGE=$\frac{\sqrt{3}}{3}$,
∴∠DGE=30°.
①如图3中,当A′D′=A′N′时,易知ND′=NN′,N′(-$\frac{5}{2}$,$\frac{5}{6}$$\sqrt{3}$).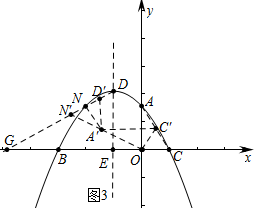
②如图4中,当N′D′=N′A′时,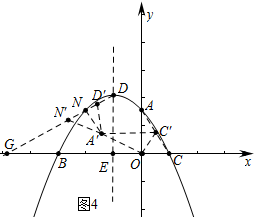
∵A′N=1,DN=$\frac{2\sqrt{3}}{3}$,
在Rt△A′N′N中,A′N′=N′D′=$\frac{2\sqrt{3}}{3}$,A′N=1,NN′=$\frac{\sqrt{3}}{3}$,
∴N′(-$\frac{5}{2}$,$\frac{5}{6}$$\sqrt{3}$).
③如图5中,延长C′A′交DG于N′,此时△D′N′A′是等腰三角形.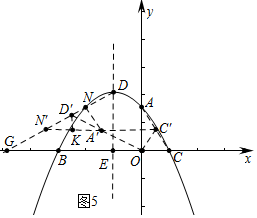
理由:作D′K⊥C′N′于K,易知N′(-$\frac{7}{2}$,$\frac{\sqrt{3}}{2}$),
∴A′N′=2,
在Rt△D′N′K中,∵∠D′N′K=30°,D′N′=$\frac{2\sqrt{3}}{3}$,
∴D′K=$\frac{\sqrt{3}}{3}$,KN′=1,
∴KA′=A′N′-N′K=2-1=1,
在Rt△A′D′K中,A′D′=$\sqrt{{1}^{2}+(\frac{\sqrt{3}}{3})^{2}}$=$\frac{2\sqrt{3}}{3}$,
∴D′N′=D′A′,
∴△A′D′N′是等腰三角形,
综上所述,当点N′的坐标为(-$\frac{5}{2}$,$\frac{5}{6}$$\sqrt{3}$)或(-$\frac{7}{2}$,$\frac{\sqrt{3}}{2}$)时,△A′D′N′是等腰三角形.
点评 本题考查二次函数综合题、一次函数的应用、垂线段最短、直角三角形30度角性质、勾股定理等知识,解题的关键是灵活运用所学知识解决问题,学会用分类讨论的思想思考问题,学会添加常用辅助线,利用垂线段最短解决最短问题,属于中考压轴题.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:选择题
 将一些相同的图形“●”按如图所示的规律依次摆放,观察每个图形中“●”的个数,若第n个图形中有3008个“●”,则n的值是( )
将一些相同的图形“●”按如图所示的规律依次摆放,观察每个图形中“●”的个数,若第n个图形中有3008个“●”,则n的值是( )| A. | 996 | B. | 999 | C. | 1001 | D. | 1002 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -9+45+28-31 | B. | 31-45-9+28 | C. | 28-9-31-45 | D. | 45-9-28+31 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
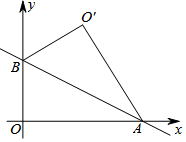 如图,直线y=-$\frac{{\sqrt{3}}}{3}$x+2与x轴,y轴分别交于A,B两点,把△AOB沿着直线AB翻折后得到△AO'B,则点O'的坐标是( )
如图,直线y=-$\frac{{\sqrt{3}}}{3}$x+2与x轴,y轴分别交于A,B两点,把△AOB沿着直线AB翻折后得到△AO'B,则点O'的坐标是( )| A. | $({\sqrt{3}\;,\;\;3})$ | B. | $({3\;,\;\;\sqrt{3}})$ | C. | $({2\;,\;\;2\sqrt{3}})$ | D. | $({2\sqrt{3}\;,\;\;4})$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com