
【题目】解下列方程
![]()
![]() ;
;
![]() .
.
【答案】![]() ,
,![]() ;
;![]() ,
,![]() .
.![]() ,
,![]() .
.
【解析】
(1)先移项,再利用平方差公式分解因式,可得方程3x+1=0和x﹣3=0,求解即可;
(2)观察原方程,方程左边可进行因式分解,因此利用因式分解法进行求解较简单;
(3)先变成标准形式,再求出b2﹣4ac的值,代入公式x=![]() ,即可求出答案.
,即可求出答案.
(1)移项得:(x+2)2﹣(2x﹣1)2=0
分解因式得:(x+2+2x﹣1)(x+2﹣2x+1)=0
整理得:(3x+1)(﹣x+3)=0
∴3x+1=0,x﹣3=0
∴ x1=﹣![]() ,x2=3
,x2=3
∴原方程的解是x1=﹣![]() ,x2=3.
,x2=3.
(2)x2+5x+6=0,即(x+2)(x+3)=0,∴x+2=0,x+3=0,解方程得:x1=﹣2,x2=﹣3,∴原方程的解是x1=﹣2,x2=﹣3.
(3)3x2+10x+5=0,这里a=3,b=10,c=5,∴△=b2﹣4ac=102﹣4×3×5=40,∴x=![]() ,∴x1=
,∴x1=![]() ,x2=
,x2=![]() ,∴原方程的解是x1=
,∴原方程的解是x1=![]() ,x2=
,x2=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,已知![]() ,按如下步骤作图:
,按如下步骤作图:
①分别以![]() 、
、![]() 为圆心,以大于
为圆心,以大于![]() 的长为半径在
的长为半径在![]() 两边作弧,交于两点
两边作弧,交于两点![]() 、
、![]() ;
;
②作直线![]() ,分别交
,分别交![]() 、
、![]() 于点
于点![]() 、
、![]() ;
;
③过![]() 作
作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() .
.
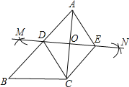
![]() 求证:四边形
求证:四边形![]() 是菱形;
是菱形;
![]() 当
当![]() ,
,![]() ,
,![]() ,求四边形
,求四边形![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着几何部分的学习,小鹏对几何产生了浓厚的兴趣,他最喜欢利用手中的工具画图了![]() 如图,作一个
如图,作一个![]() ,以O为圆心任意长为半径画弧分别交OA,OB于点C和点D,将一副三角板如图所示摆放,两个直角三角板的直角顶点分别落在点C和点D,直角边中分别有一边与角的两边重合,另两条直角边相交于点P,连接
,以O为圆心任意长为半径画弧分别交OA,OB于点C和点D,将一副三角板如图所示摆放,两个直角三角板的直角顶点分别落在点C和点D,直角边中分别有一边与角的两边重合,另两条直角边相交于点P,连接![]() 小鹏通过观察和推理,得出结论:OP平分
小鹏通过观察和推理,得出结论:OP平分![]() .
.
你同意小鹏的观点吗?如果你同意小鹏的观点,试结合题意写出已知和求证,并证明.
已知:![]() 中,______
中,______![]() ______,______
______,______![]() ______,______
______,______![]() ______.
______.
求证:OP平分![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】快、慢两车分别从相距360km的佳市、哈市两地出发,匀速行驶,先相向而行,慢车在快车出发1h后出发,到达佳市后停止行驶,快车到达哈市后,立即按原路原速返回佳市(快车调头的时间忽略不计),快、慢两车距哈市的路程y1(单位:km),y2(单位:km)与快车出发时间x(单位:h)之间的函数图象如图所示,请结合图象信息解答下列问题:
(1)直接写出慢车的行驶速度和a的值;
(2)快车与慢车第一次相遇时,距离佳市的路程是多少千米?
(3)快车出发多少小时后两车相距为100km?请直接写出答案.
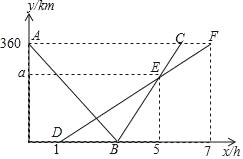
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(﹣1,5)、B(﹣1,0)、C(﹣4,3).

(1)请画出△ABC关于y轴对称的△DEF(其中D、E、F分别是A、B、C的对应点).
(2)直接写出(1)中F点的坐标为 .
(3)若直线l经过点(0,﹣2)且与x轴平行,则点C关于直线l的对称点的坐标为 .
(4)在y轴上存在一点P,使PC﹣PB最大,则点P的坐标为 .
(5)第一象限有一点M(4,2),在x轴上找一点Q使CQ+MQ最短,画出最短路径,保留作图痕迹.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,每个小正方形的边长为1,点A的坐标为(-3,2).请按要求分别完成下列各小题:
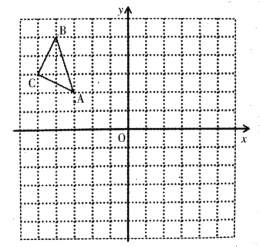
(1)把△ABC向下平移4个单位得到△A1B1C1,画出△A1B1C1,点A1的坐标是___.
(2)画出△ABC关于y轴对称的△A2B2C2,则点C2的坐标是 ;
(3)△ABC的面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,点E为边AB上任意一点,点D在边CB的延长线上,且ED=EC.

(1)当点E为AB的中点时(如图1),则有AE DB(填“>”“<”或“=”);
(2)猜想AE与DB的数量关系,并证明你的猜想.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com