
【题目】平面直角坐标系中,直线 ![]() 与x轴交于点A ,与y 轴交于点B,直线
与x轴交于点A ,与y 轴交于点B,直线 ![]() 与x轴交于点C,与直线
与x轴交于点C,与直线![]() 交于点P.
交于点P.
(1)当k=1 时,求点C的坐标;
(2)如图 1,点D为PA的中点,过点D作DE⊥x轴于E,交直线![]() 于点F,若DF=2DE,求k的值;
于点F,若DF=2DE,求k的值;
(3)如图2,点P在第二象限内,PM⊥x轴于M,以PM为边向左作正方形PMNQ,NQ 的延长线交直线![]() 于点R,若PR=PC,求点P的坐标.
于点R,若PR=PC,求点P的坐标.


【答案】(1)(-2,0)(2)![]() (3)(-
(3)(-![]() ,
,![]() )
)
【解析】(1)解两个函数解析式组成的方程组即可求解;
(2)过点P作PG⊥DF于点G,易证△PDG≌△ADE,过点P作PH⊥CA于点H,可证点H是AC中点,则H的坐标即可求得,进而求得点P的坐标,再求得点K的值即可;
(3)Rt△PMC≌Rt△PQR,则RQ=MC,设NR=NC=a,则R(﹣a﹣2,a),代入y=﹣![]() x+3,求得a的值,设P(m,n),根据P在直线l1上和RQ=MC即可列方程组求解.
x+3,求得a的值,设P(m,n),根据P在直线l1上和RQ=MC即可列方程组求解.
(1)当k=1时,直线l2为y=x+2.
解方程组 ,
,
解得![]() ,
,
∴P(![]() ,
,![]() );
);
(2)当y=0时,kx+2k=0,
∵k≠0,
∴x=﹣2,
∴C(﹣2,0)则OC=2,
当y=0时,﹣![]() x+3=0,
x+3=0,
∴x=6,
∴A(6,0),OA=6,
过点P作PG⊥DF于点G,
在△PDG和△ADE中,
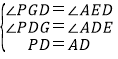 ,
,
∴△PDG≌△ADE,
得DE=DG=![]() DF,
DF,
∴PD=PF,
∴∠PFD=∠PDF
∵∠PFD+∠PCA=90°,∠PDF+∠PAC=90°
∴∠PCA=∠PAC,
∴PC=PA
过点P作PH⊥CA于点H,
∴CH=![]() CA=4,
CA=4,
∴OH=2,
当x=2时,y=﹣![]() ×2+3=2代入y=kx+2k,得k=
×2+3=2代入y=kx+2k,得k=![]() ;
;
(3)直角△PQR和直角△PMC中,
![]() ,
,
∴Rt△PMC≌Rt△PQR,
∴CM=RQ,
∴NR=NC,
设NR=NC=a,则R(﹣a﹣2,a),
代入y=﹣![]() x+3,
x+3,
得﹣![]() (﹣a﹣2)+3=a,解得a=8,
(﹣a﹣2)+3=a,解得a=8,
设P(m,n),则 ,
,
解得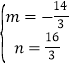 ,
,
∴P(![]() ,
,![]() ).
).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,Rt△ABC的三个顶点分别是A(﹣3,2),B(0,4),C(0,2). 
(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C;
(2)平移△ABC,若点A的对应点A2的坐标为(0,﹣4),画出平移后对应的△A2B2C2;
(3)若将△A1B1C绕某一点旋转可以得到△A2B2C2;请在坐标系中作出旋转中心S并写出旋转中心S的坐标:S
(4)在x轴上有一点P,使得PA+PB的值最小,请作图标出P点并写出点P的坐标.P .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设计调查问卷时,下列提问是否合适?如果不合适的话应该怎样改进?
(1)你上学时使用的交通工具是
![]() .汽车
.汽车![]() .摩托车
.摩托车![]() .步行
.步行![]() .其他
.其他
(2)你对老师的教学满意吗?
![]() .比较满意
.比较满意![]() .满意
.满意![]() .非常满意.
.非常满意.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=﹣2x2+(m+9)x﹣6的对称轴是x=2.
(1)求抛物线表达式和顶点坐标;
(2)将该抛物线向右平移1个单位,平移后的抛物线与原抛物线相交于点A,求点A的坐标;
(3)抛物线y=﹣2x2+(m+9)x﹣6与y轴交于点C,点A关于平移后抛物线的对称轴的对称点为点B,两条抛物线在点A、C和点A、B之间的部分(包含点A、B、C) 记为图象M.将直线y=2x﹣2向下平移b(b>0)个单位,在平移过程中直线与图象M始终有两个公共点,请你写出b的取值范围 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是等边△ABC内的一点,且PA=5,PB=4,PC=3,将△APB绕点B逆时针旋转,得到△CQB.求: 
(1)点P与点Q之间的距离;
(2)求∠BPC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义一种对正整数n的“F”运算:①当n为奇数时,F(n)=3n+1;②当n为偶数时,F(n)=![]() (其中k是使F(n)为奇数的正整数)……,两种运算交替重复进行,例如,取n=24,则:
(其中k是使F(n)为奇数的正整数)……,两种运算交替重复进行,例如,取n=24,则:
![]()
若n=13,则第2018次“F”运算的结果是( )
A. 1 B. 4 C. 2018 D. 42018
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读资料:
如图1,在平面直角坐标系xOy中,A,B两点的坐标分别为A(x1 , y1),B(x2 , y2),由勾股定理得AB2=|x2﹣x1|2+|y2﹣y1|2 , 所以A,B两点间的距离为AB= ![]() .
.
我们知道,圆可以看成到圆心的距离等于半径的点的集合,如图2,在平面直角坐标系xOy中,A (x,y)为圆上任意一点,则点A到原点的距离的平方为OA2=|x﹣0|2+|y﹣0|2 , 当⊙O的半径OA为r时,⊙O的方程可写为:x2+y2=r2 .
问题拓展:
如果圆心坐标为P (a,b),半径为r,那么⊙P的方程可以写为 (x﹣a)2+(y﹣b)2=r2 .
综合应用:
如图3,⊙P与x轴相切于原点O,P点坐标为(0,6),A是⊙P上一点,连接OA,使∠POA=30°,作PD⊥OA,垂足为D,延长PD交x轴于点B,连接AB.
①证明AB是⊙P的切线;
②是否存在到四点O,P,A,B距离都相等的点Q?若存在,求Q点坐标,并写出以点Q为圆心,OQ长为半径的⊙Q的方程;若不存在,说明理由.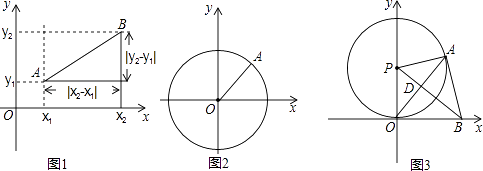
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com