
【题目】已知⊙O的半径为10cm,弦AB∥CD,AB=12cm,CD=16cm,则AB和CD的距离为( )
A.2cm
B.14cm
C.2cm或14cm
D.10cm或20cm
【答案】C
【解析】解:①AB,CD在圆心的同侧如图(一),连接OD,OB,过O作AB的垂线交CD、AB于E,F, 根据垂径定理得ED= ![]() CD=
CD= ![]() ×16=8cm,FB=
×16=8cm,FB= ![]() AB=
AB= ![]() ×12=6cm,
×12=6cm,
在Rt△OED中,OD=10cm,ED=8cm,由勾股定理得OE= ![]() =
= ![]() =6(cm),
=6(cm),
在Rt△OFB中,OB=10cm,FB=6cm,则OF= ![]() =
= ![]() =8(cm),
=8(cm),
AB和CD的距离是OF﹣OE=8﹣6=2(cm);
②AB,CD在圆心的异侧如图(二),连接OD,OB,过O作AB的垂线交CD、AB于E,F,
根据垂径定理得ED= ![]() CD=
CD= ![]() ×16=8cm,FB=
×16=8cm,FB= ![]() AB=
AB= ![]() ×12=6cm,
×12=6cm,
在Rt△OED中,OD=10cm,ED=8cm,由勾股定理得OE= ![]() =
= ![]() =6(cm),
=6(cm),
在Rt△OFB中,OB=10cm,FB=6cm,则OF= ![]() =
= ![]() =8(cm),
=8(cm),
AB和CD的距离是OF+OE=6+8=14(cm),
AB和CD的距离是2cm或14cm.
故选C.
【考点精析】关于本题考查的勾股定理的概念和垂径定理,需要了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧才能得出正确答案.


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:初中数学 来源: 题型:
【题目】某宾馆客房部有60个房间供游客居住,当每个房间的定价为每天200元时,房间可以住满.当每个房间每天的定价每增加10元时,就会有一个房间空闲.对有游客入住的房间,宾馆需对每个房间每天支出20元的各种费用. 设每个房间每天的定价增加x元.求:
(1)房间每天的入住量y(间)关于x(元)的函数关系式;
(2)该宾馆每天的房间收费p(元)关于x(元)的函数关系式;
(3)该宾馆客房部每天的利润w(元)关于x(元)的函数关系式;当每个房间的定价为每天多少元时,w有最大值?最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为丰富居民业余生活,某居民区组建筹委会,该筹委会动员居民自愿集资建立一个书刊阅览室.经预算,一共需要筹资30000元,其中一部分用于购买书桌、书架等设施,另一部分用于购买书刊.
(1)筹委会计划,购买书刊的资金不少于购买书桌、书架等设施资金的3倍,问最多用多少资金购买书桌、书架等设施?
(2)经初步统计,有200户居民自愿参与集资,那么平均每户需集资150元.镇政府了解情况后,赠送了一批阅览室设施和书籍,这样,只需参与户共集资20000元.经筹委会进一步宣传,自愿参与的户数在200户的基础上增加了a%(其中a>0).则每户平均集资的资金在150元的基础上减少了 ![]() a%,求a的值.
a%,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数 ![]() 的图象经过点
的图象经过点 ![]() ,若一次函数y=x+1的图象平移后经过该反比例函数图象上的点B(2,m),求平移后的一次函数图象与x轴的交点坐标.
,若一次函数y=x+1的图象平移后经过该反比例函数图象上的点B(2,m),求平移后的一次函数图象与x轴的交点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图某超市举行“翻牌”抽奖活动,在一张木板上共有6个相同的牌,其分别对应价值为2元、5元、8元、10元、20元和50元的奖品. 
(1)小雷在该抽奖活动中随机翻一张牌,求抽中10元奖品的概率;
(2)如果随机翻两张牌,且第一次翻过的牌不再参加下次翻牌,求两次抽中的奖品的总价值大于14元的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1个单位长度的小正方形组成的网格中,建立如图所示的平面直角坐标系,请按要求完成下面的问题:
(1)以图中的点O为位似中心,将△ABC作位似变换且同向放大到原来的两倍,得到△A1B1C1;
(2)若△ABC内一点P的坐标为(a,b),则位似变化后对应的点P′的坐标是 . 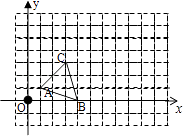
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com