
如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD,等边△ABE.已知∠BAC=30°,EF⊥AB,垂足为F,连接DF.
(1)试说明AC=EF;
(2)求证:四边形ADFE是平行四边形.

证明见解析.
【解析】
试题分析:(1)一方面Rt△ABC中,由∠BAC=30°可以得到AB=2BC,另一方面△ABE是等边三角形,EF⊥AB,由此得到AE=2AF,并且AB=2AF,从而可证明△AFE≌△BCA,再根据全等三角形的性质即可证明AC=EF.
(2)根据(1)知道EF=AC,而△ACD是等边三角形,所以EF=AC=AD,并且AD⊥AB,而EF⊥AB,由此得到EF∥AD,再根据平行四边形的判定定理即可证明四边形ADFE是平行四边形.
试题解析:证明:(1)∵Rt△ABC中,∠BAC=30°,∴AB=2BC.
又∵△ABE是等边三角形,EF⊥AB,∴AB=2AF.∴AF=BC.
∵在Rt△AFE和Rt△BCA中,AF=BC,AE=BA,
∴△AFE≌△BCA(HL).∴AC=EF.
(2)∵△ACD是等边三角形,∴∠DAC=60°,AC=AD.
∴∠DAB=∠DAC+∠BAC=90°.∴EF∥AD.
∵AC=EF,AC=AD,∴EF=AD.
∴四边形ADFE是平行四边形.
考点:1.全等三角形的判定与性质;2.等边三角形的性质;3.平行四边形的判定.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:初中数学 来源:2014-2015山东省威海市环翠区七年级上学期期中考试数学试卷(解析版) 题型:选择题
下列几何图形中,对称轴条数最多的是( )
(A)等腰三角形 (B)正方形 (C)等腰梯形 (D)长方形
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(四川凉山卷)数学(解析版) 题型:选择题
如图,河堤横断面迎水坡AB的坡比是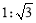 ,堤高BC=10m,则坡面AB的长度是( )
,堤高BC=10m,则坡面AB的长度是( )

A.15m B. C.20m D.
C.20m D.
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(四川凉山卷)数学(解析版) 题型:解答题
我州某校计划购买甲、乙两种树苗共1000株用以绿化校园,甲种树苗每株25元,乙种树苗每株30元,通过调查了解,甲,乙两种树苗成活率分别是90%和95%.
(1)若购买这种树苗共用去28000元,则甲、乙两种树苗各购买多少株?
(2)要使这批树苗的总成活率不低于92%,则甲种树苗最多购买多少株?
(3)在(2)的条件下,应如何选购树苗,使购买树苗的费用最低?并求出最低费用.
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(广东卷)数学(解析版) 题型:解答题
如图,⊙ 是△ABC的外接圆,AC是直径,过点O作OD⊥AB于点D,延长DO交⊙
是△ABC的外接圆,AC是直径,过点O作OD⊥AB于点D,延长DO交⊙ 于点P,过点P作PE⊥AC于点E,作射线DE交BC的延长线于F点,连接PF。
于点P,过点P作PE⊥AC于点E,作射线DE交BC的延长线于F点,连接PF。

(1)若∠POC=60°,AC=12,求劣弧PC的长;(结果保留π)
(2)求证:OD=OE;
(3)求证:PF是⊙ 的切线。
的切线。
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(浙江嘉兴卷)数学(解析版) 题型:选择题
一名射击爱好者5次射击的中靶环数如下:6,7,9,8,9.这5个数据的中位数是( )
A.6 B.7 C.8 D.9
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com