Question

我州某校计划购买甲、乙两种树苗共1000株用以绿化校园，甲种树苗每株25元，乙种树苗每株30元，通过调查了解，甲，乙两种树苗成活率分别是90%和95%．

（1）若购买这种树苗共用去28000元，则甲、乙两种树苗各购买多少株？

（2）要使这批树苗的总成活率不低于92%，则甲种树苗最多购买多少株？

（3）在（2）的条件下，应如何选购树苗，使购买树苗的费用最低？并求出最低费用．

 

Answer 1

（1）购甲种树苗400株，乙种树苗600株；（2）甲种树苗最多购买600株；（3）购买家中树苗600株．乙种树苗400株时总费用最低，最低费用为27000元．

【解析】

试题分析：（1）方程组的应用解题关键是设出未知数，找出等量关系，列出方程组求解．本题设购甲种树苗x株，乙种树苗y株，根据购买甲、乙两种树苗共1000株和购买两种树苗的总价为28000元建立方程组求出其解即可．

（2）不等式的应用解题关键是找出不等量关系，列出不等式求解．本题设购买甲种树苗a株，则购买乙种树苗（1000﹣a）株，由这批树苗的总成活率不低于92%建立不等式求出其解即可．

（3）设购买树苗的总费用为W元，根据总费用=两种树苗的费用之和建立解析式，由一次函数的性质求出结论．

试题解析：【解析】
（1）设购甲种树苗x株，乙种树苗y株，由题意，得

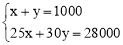，解得：．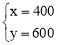

答：购甲种树苗400株，乙种树苗600株．

（2）设购买甲种树苗a株，则购买乙种树苗（1000﹣a）株，由题意，得

90%a+95%（1000﹣a）≥92%×1000，解得：a≤600．

答：甲种树苗最多购买600株．

（3）设购买树苗的总费用为W元，由题意，得

W=25a+30（1000﹣a）=﹣5a+30000．

∵k=﹣5＜0，∴W随a的增大而减小，

∵0＜a≤600，∴a=600时，W最小=27000元．

∴购买家中树苗600株．乙种树苗400株时总费用最低，最低费用为27000元．

考点：1．二元一次方程组的应用；2．一元一次不等式的应用；3．一次函数的应用．