
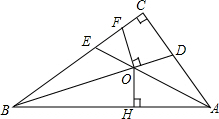
 已知如图:Rt△ABC中,∠ACB=90°,AE平分∠BAC,BD平分∠ABC,AE、BD相交于O,OF⊥BD,OH⊥AB,下列结论:①OE平分∠BOF;②BF+AD=AB;③OF=OD;④$\frac{CF+CD}{OH}$为定值,成立的有( )
已知如图:Rt△ABC中,∠ACB=90°,AE平分∠BAC,BD平分∠ABC,AE、BD相交于O,OF⊥BD,OH⊥AB,下列结论:①OE平分∠BOF;②BF+AD=AB;③OF=OD;④$\frac{CF+CD}{OH}$为定值,成立的有( )| A. | ①②③④ | B. | ②④ | C. | ①③ | D. | ①②④ |
分析 ①要想证明OE平分∠BOF,就要证明∠BOE=∠EOF,利用对顶角相等的性质,找到∠MOA和∠DOA,易证∠MOA=∠DOA,结论正确;②③④均由①中得证得结论推导出;故最终答案①②③④均正确.
解答 解:如图,①延长EO交AB于点M,作OI⊥BC,OG⊥AC,
∵AE平分∠BAC,BD平分∠ABC,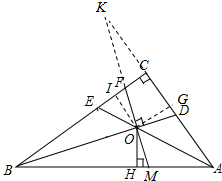
∴OI=OH,
∵OF⊥BD,
∴∠BFO=∠BMO,
∴△OIF≌△OHM(AAS),
∴∠IOF=∠HOM,
∵∠IOF+∠FOG=∠DOG+∠FOG=90°,
∴∠IOF=∠GOD,
∴∠HOM=∠GOD,
∴△OHM≌△OGM(AAS),
∴∠MOA=∠DOA=∠EOF=∠EOB(对顶角相等),
∴OE平分∠BOF,
故①正确;
②由①知,BF=BM,AD=AM,
∴BF+AD=BM+AM=AB,
故②正确;
③由①知,OF=OM=OD,
故③正确;
④延长AC,OF交于点K,易知,
△KCF∽△KGO,△BOI∽△BDC,
∴$\frac{CF}{OG}$和$\frac{CD}{OI}$是定值,
∵$\frac{CF+CD}{OH}$=$\frac{CF}{OH}+\frac{CD}{OH}=\frac{CF}{OG}+\frac{CD}{OI}$,
∴$\frac{CF+CD}{OH}$为定值,
故④正确.
故答案选:A.
点评 本题考查了全等三角形的判定与性质,等腰三角形的判定,对顶角相等,相似比为定值最终判定出①②③④全部正确.解决本题的关键由三角形角平分线的性质入手,即角平分线上的点到角两边的距离相等.此题难度较大,好题.


科目:初中数学 来源: 题型:选择题
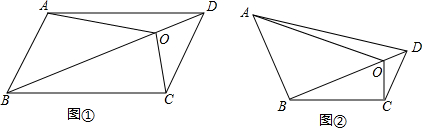
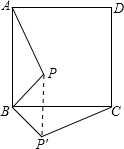 正方形ABCD内一点P,BP=2,把△ABP绕点B顺时针旋转90°得到△CBP′,则PP′的长为( )
正方形ABCD内一点P,BP=2,把△ABP绕点B顺时针旋转90°得到△CBP′,则PP′的长为( )| A. | 2$\sqrt{2}$ | B. | 2$\sqrt{3}$ | C. | 3 | D. | 3$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
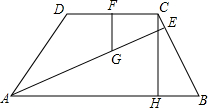 如图,在等腰梯形ABCD中,AB∥CD,AB=4,CD=2,CH⊥AB于点H,AE⊥BC于点E,CE:EB=1:4,F是CD上一点,FG⊥CD于点G.
如图,在等腰梯形ABCD中,AB∥CD,AB=4,CD=2,CH⊥AB于点H,AE⊥BC于点E,CE:EB=1:4,F是CD上一点,FG⊥CD于点G.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com