
分析 (1)把A(2,0)代入C1得到a(2-t-2)2+t2=0,根据a≠0,t≠0,可求a的结果;
(2)根据平移的性质可得C2:y=-(x-2)2+t2,根据判别式可得t的值,从而得到抛物线C2解析式;
(3)由(2)把t=2代入①得x=1,得M(1,3),N(2,4),则直线NA是对称轴,分两种情况:①作MQ1⊥NA于B交抛物线于点Q1,②若∠NMQ2=90°,作MH⊥x轴于点C.进行讨论可求点Q的坐标.
解答 解:(1)把A(2,0)代入C1得到:a(2-t-2)2+t2=0,
即(1+a)t2=0,
∵a≠0,t≠0,
∴a=-1;
(2)由(1)得C1:y=-(x-t-2)2+t2,
∵把抛物线C1向左平移t个单位后得抛物线C2,
∴C2:y=-(x-2)2+t2,
令-(x-2)2+t2=2x+1,
整理得x2-2x+5-t2=0,①
∵抛物线C2与直线l有唯一公共点M,
∵△=4-4×1×(5-t2)=0,
∴t2=4,
∵t>0,
∴t=2,
∴抛物线C2解析式为:y=-(x-2)2+4;
(3)存在点Q,使△MNQ是直角三角形,
由(2)把t=2代入①得x=1,得M(1,3),N(2,4),则直线NA是对称轴,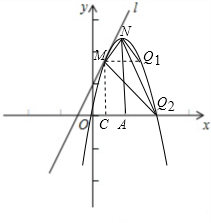 ①作MQ1⊥NA于B交抛物线于点Q1,
①作MQ1⊥NA于B交抛物线于点Q1,
∵MB=BQ1=NB=1,
∴∠MNQ1=90°,
∴Q1(3,3);
②若∠NMQ2=90°,作MH⊥x轴于点C.
∵∠NMQ1=45°,
∴∠Q2MQ1=45°,
∴∠CMQ2=∠CQ2M=45°,
∴CM=CQ2,
设Q(m,-m2+4m),
∴m-1=3-(-m2+4m),
解得m1=1(舍去),m2=4,
∴Q2(4,0)
综上所述,存在点Q1(3,3),Q2(4,0),使△MNQ是直角三角形.
点评 此题考查了抛物线解析式的确定,平移的性质,判别式,直角三角形的性质等重要知识点,(3)小题中,都用到了分类讨论的数学思想,难点在于考虑问题要全面,做到不重不漏.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
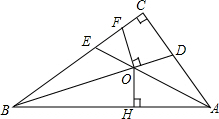 已知如图:Rt△ABC中,∠ACB=90°,AE平分∠BAC,BD平分∠ABC,AE、BD相交于O,OF⊥BD,OH⊥AB,下列结论:①OE平分∠BOF;②BF+AD=AB;③OF=OD;④$\frac{CF+CD}{OH}$为定值,成立的有( )
已知如图:Rt△ABC中,∠ACB=90°,AE平分∠BAC,BD平分∠ABC,AE、BD相交于O,OF⊥BD,OH⊥AB,下列结论:①OE平分∠BOF;②BF+AD=AB;③OF=OD;④$\frac{CF+CD}{OH}$为定值,成立的有( )| A. | ①②③④ | B. | ②④ | C. | ①③ | D. | ①②④ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{9}{25}$ | B. | $\frac{12}{5}$ | C. | $\frac{9}{10}$ | D. | $\frac{9}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com