
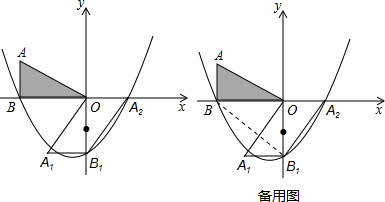
���� ��1�����ȸ�����ת������ȷ����B��B1��A2��������꣬Ȼ�����ô���ϵ������������ߵĽ���ʽ��
��2�����PBB1����ķ�������ͼ1��ʾ�������PBB1���������ʽ��S��PBB1=S��PBC+S�ı���PCOB1-S��OBB1�������ó��𰸣�
��3�����������ˣ�2�������������������ʽ�Ľ��ۣ����ô˱���ʽ��ʾ����QBB1�������Ȼ���һԪ���η������Q������꣮
���  �⣺��1����AB��x�ᣬAB=6��tan��AOB=$\frac{3}{4}$��
�⣺��1����AB��x�ᣬAB=6��tan��AOB=$\frac{3}{4}$��
��OB=8��
��B��-8��0����B1��0��-8����A2��6��0����
��������y=a��x+8����x-6����a��0��������B1��0��-8����
��$a=\frac{1}{6}$��
�������ߵĽ���ʽΪ��$y=\frac{1}{6}{x^2}+\frac{1}{3}x-8$��
��2����P�ǵ���������������$y=\frac{1}{6}{x^2}+\frac{1}{3}x-8$�ϵ�һ�㣬
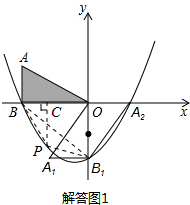
���ͼ1������P��PC��x���ڵ�C��
���P��������m��n������m��0��n��0��$n=\frac{1}{6}{m^2}+\frac{1}{3}m-8$��
����PC=|n|=-n=$-\frac{1}{6}{m^2}-\frac{1}{3}m+8$��OC=|m|=-m��
BC=OB-OC=4+m��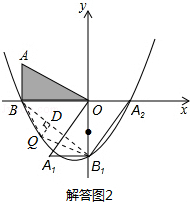
S��PBB1=S��PBC+S�ı���PCOB1-S��OBB1=-$\frac{2}{3}$m2-$\frac{16}{3}$m��
��3�������ڵ��������������ϴ��ڵ㣬ʹ��Q��x1��y1�����߶�BB1�ľ���Ϊ$\sqrt{2}$��
���ͼ2������Q��QD��BB1�ڵ�D��
�ɣ�2����֪����ʱ��QBB1��������Ա�ʾΪ��$-\frac{2}{3}{x_1}^2-\frac{16}{3}{x_1}$��
��Rt��QBB1��BB1=$\sqrt{O{B}^{2}+O{B}_{1}^{2}}$=$8\sqrt{2}$
��S��QBB1=$\frac{1}{2}��QD��B{B_1}$=$\frac{1}{2}��8\sqrt{2}��\sqrt{2}$=8��
��$-\frac{2}{3}{x_1}^2-\frac{16}{3}{x_1}=8$��
��ã�x1=-2��x1=-6
��x1=-2ʱ��y1=-8����x1=-6ʱ��y1=-4��
��Q��-2��-8����Q��-6��-4����
���� ���⿼���˴���ϵ�����������߽���ʽ�����κ���ͼ���ϵ������������һԪ���η��̡���ת������仯��ͼ����������ɶ�������Ҫ֪ʶ�㣮�ڣ�2������������µ����ã��DZ�����ѵ�����ģ����е�Ҫ��������ƽ����ͼ���������ⷽ�������ַ�����ѹ�����г�����һ�ֽ��ⷽ����ͬѧ����Ҫ�������գ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
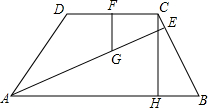 ��ͼ���ڵ�������ABCD�У�AB��CD��AB=4��CD=2��CH��AB�ڵ�H��AE��BC�ڵ�E��CE��EB=1��4��F��CD��һ�㣬FG��CD�ڵ�G��
��ͼ���ڵ�������ABCD�У�AB��CD��AB=4��CD=2��CH��AB�ڵ�H��AE��BC�ڵ�E��CE��EB=1��4��F��CD��һ�㣬FG��CD�ڵ�G���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
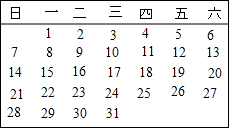 ��ͼ��ij�µ����������Ż�����ȡ�������������֣����ǵĺͿ����ǣ�������
��ͼ��ij�µ����������Ż�����ȡ�������������֣����ǵĺͿ����ǣ�������| A�� | 18 | B�� | 33 | C�� | 38 | D�� | 81 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
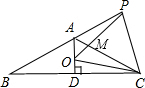 ��ͼ����֪������ABC�У�AB=AC����BAC=120�㣬AD��BC�ڵ�D����P��BA�ӳ�����һ�㣬��O���߶�AD��һ�㣬OP=OC������Ľ��ۣ��١�APO+��DCO=30�㣻�ڡ�OPC�ǵȱ������Σ���AC=AO+AP����S��ABC=S�ı���AOCP��������ȷ�ĸ����ǣ�������
��ͼ����֪������ABC�У�AB=AC����BAC=120�㣬AD��BC�ڵ�D����P��BA�ӳ�����һ�㣬��O���߶�AD��һ�㣬OP=OC������Ľ��ۣ��١�APO+��DCO=30�㣻�ڡ�OPC�ǵȱ������Σ���AC=AO+AP����S��ABC=S�ı���AOCP��������ȷ�ĸ����ǣ�������| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com