
【题目】有n个数,第一个记为a1,第二个.记为a2;……,第n个记为ax,若 a1=![]() ,且从第二个数起,每个数都等于“1与它前面那个数的差的倒数”
,且从第二个数起,每个数都等于“1与它前面那个数的差的倒数”
(1)则a2=______;a3 =______;a4 =______.
(2)根据(1)的计算结果,猜想a2005=______;a2006=______.
(3)计算: ![]() 的值.
的值.
【答案】 2 -1 ![]() 2 1
2 1
【解析】试题分析:(1)根据从第二个数起,每个数都等于“1与它前面那个数的差的倒数”进行计算,分别求出a2,a3,a4;
(2)根据(1)的计算结果得出规律:每3个数为一个循环,而求出a2004,a2005,a2006的值;
(3)通过计算出a1a2a3的值为-1,结合(1)得出的规律计算出要求的值.
试题解析:(1)∵a1=![]() ,
,
∴a2= ,a3=
,a3=![]() =-1,a4=
=-1,a4=![]() ;
;
(2)根据(1)的计算可以得到a1=a4,则这些数三个数循环一次,
2004÷3=668,则a2004=a3=![]() ;
;
2005÷3=668…1,则a2005=a1= ![]() ;
;
2006÷3=668…2,则a2006=a2=2;
(3)根据题意得:
a1a2a3…a2014a2015a2016=![]() ×2×(-1)×…×
×2×(-1)×…×![]() ×2×(-1)=1.
×2×(-1)=1.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8cm,AD=24cm,BC=26cm,动点P从点A出发,以1cm/s的速度向点D运动;动点Q从点C同时出发,以3cm/s的速度向点B运动.规定当其中一个动点到达端点时,另一个动点也随之停止运动.设运动时间为t,求: 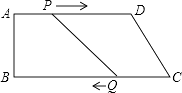
(1)当t为何值时,PQ∥CD?
(2)当t为何值时,PQ=CD?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在平面直角坐标系中,点A,B的坐标分别为(-1,0),(3,0),现同时将点A,B分别向上平移2个单位长度,再向右平移1个单位长度,分别得到点A,B的对应点C,D,连接AC,BD,CD.
(1)求点C,D的坐标及S四边形ABDC.
(2)在y轴上是否存在一点Q,连接QA,QB,使S△QAB=S四边形ABDC?若存在这样一点,求出点Q的坐标;若不存在,试说明理由.
(3)如图②,点P是线段BD上的一个动点,连接PC,PO,当点P在BD上移动时(不与B,D重合),给出下列结论:①![]() 的值不变,②
的值不变,②![]() 的值不变,其中有且只有一个是正确的,请你找出这个结论并求其值.
的值不变,其中有且只有一个是正确的,请你找出这个结论并求其值.

查看答案和解析>>
科目:初中数学 来源: 题型:
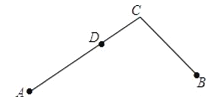
【题目】如果一点在由两条公共端点的线段组成的一条折线上且把这条折线分成长度相等的两部分,这点叫做这条折线的“折中点”.如果点D是折线A﹣C﹣B的“折中点”,请解答以下问题:
(1)已知AC=m,BC=n.
当m>n时,点D在线段 上;
当m=n时,点D与 重合;
当m<n时,点D在线段 上;
(2)若E为线段AC中点,EC=4,CD=3,求CB的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班10名学生的校服尺寸与对应人数如表所示:
尺寸(cm) | 160 | 165 | 170 | 175 | 180 |
学生人数(人) | 1 | 3 | 2 | 2 | 2 |
则这10名学生校服尺寸的众数和中位数分别为( )
A.165cm,165cm
B.165cm,170cm
C.170cm,165cm
D.170cm,170cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,矩形ABCD中,AB=7cm,AD=4cm,点E为AD上一定点,F为AD延长线上一点,且DF=acm,点P从A点出发,沿AB边向点B以2cm/s的速度运动,运动到B点停止,连结PE,设点P运动的时间为ts,△PAE的面积为ycm2 , 当0≤t≤1时,△PAE的面积y(cm2)关于时间t(s)的函数图象如图2所示,连结PF,交CD于点H.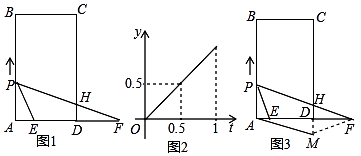
(1)t的取值范围为 , AE=cm;
(2)如图3,将△HDF沿线段DF进行翻折,与CD的延长线交于点M,连结AM,当a为何值时,四边形PAMH为菱形?
(3)在(2)的条件下求出点P的运动时间t.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如图1,点M,N把线段AB分割成AM,MN和BN,若以AM,MN,BN为边的三角形是一个直角三角形,则称点M,N是线段AB的勾股分割点. 请解决下列问题: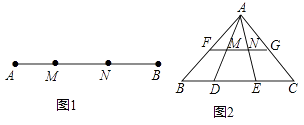
(1)已知点M,N是线段AB的勾股分割点,且BN>MN>AM.若AM=2,MN=3,求BN的长;
(2)如图2,若点F、M、N、G分别是AB、AD、AE、AC边上的中点,点D,E是线段BC的勾股分割点,且EC>DE>BD,求证:点M,N是线段FG的勾股分割点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com