
【题目】如图1,矩形ABCD中,AB=7cm,AD=4cm,点E为AD上一定点,F为AD延长线上一点,且DF=acm,点P从A点出发,沿AB边向点B以2cm/s的速度运动,运动到B点停止,连结PE,设点P运动的时间为ts,△PAE的面积为ycm2 , 当0≤t≤1时,△PAE的面积y(cm2)关于时间t(s)的函数图象如图2所示,连结PF,交CD于点H.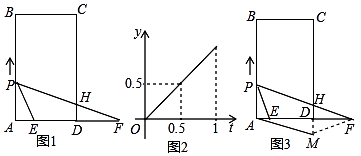
(1)t的取值范围为 , AE=cm;
(2)如图3,将△HDF沿线段DF进行翻折,与CD的延长线交于点M,连结AM,当a为何值时,四边形PAMH为菱形?
(3)在(2)的条件下求出点P的运动时间t.
【答案】
(1)0≤t≤3.5;1
(2)
解:如图3,

∵四边形AMHP是菱形,
∴AM=MH=2DM,AM∥PF,
∵∠ADM=90°,DM= ![]() AM,
AM,
∴∠MAD=30°,
∴∠PFA=MFA=∠MAD=30°,
∴MA=MF,
∵MD⊥AF,
∴AD=DF=4,
∴a=4.
(3)
解:当a=4cm时,FA=AD+DF=8cm,
令PA=x,则PF=2x,
根据勾股定理可得,PF2=PA2+AF2,
即(2x)2=x2+82,
解得x= ![]() ,(负值已舍去)
,(负值已舍去)
∴P的运动时间为 ![]() ÷2=
÷2= ![]() 秒
秒
【解析】解:(1)∵AB=7,而7÷2=3.5,
∴0≤t≤3.5,
由题意可知,y= ![]() ×2t×AE,
×2t×AE,
由图2可知,当t=0.5时,y=0.5,
∴0.5= ![]() ×2×0.5×AE,
×2×0.5×AE,
∴AE=1,
故答案分别为:0≤t≤3.5,1;
(1)根据AB的长以及点P的移动速度,可以确定t的范围;根据题意可知,y= ![]() ×2t×AE,由图2可知,当t=0.5时,y=0.5,进而得出0.5=
×2t×AE,由图2可知,当t=0.5时,y=0.5,进而得出0.5= ![]() ×2×0.5×AE,即可求出AE.(2)根据菱形的性质以及轴对称的性质,即可证明∠MAD=∠MFD=30°,最后根据等腰三角形的性质,即可解决问题.(3)令PA=x,则PF=2x,根据勾股定理可得,PF2=PA2+AF2 , 即可得出方程(2x)2=x2+82 , 求得x的值即可得到点P的运动时间t.
×2×0.5×AE,即可求出AE.(2)根据菱形的性质以及轴对称的性质,即可证明∠MAD=∠MFD=30°,最后根据等腰三角形的性质,即可解决问题.(3)令PA=x,则PF=2x,根据勾股定理可得,PF2=PA2+AF2 , 即可得出方程(2x)2=x2+82 , 求得x的值即可得到点P的运动时间t.


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案科目:初中数学 来源: 题型:
【题目】“4000辆自行车、187个服务网点”,台州市区现已实现公共自行车服务全覆盖,为人们的生活带来了方便.图①是公共自行车的实物图,图②是公共自行车的车架示意图,点A、D、C、E在同一条直线上,CD=30cm,DF=20cm,AF=25cm,FD⊥AE于点D,座杆CE=15cm,且∠EAB=75°.
(1)求AD的长;
(2)求点E到AB的距离.(参考数据:sin75°≈0.97,cos75°≈0.26,tan75°≈3.73)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有n个数,第一个记为a1,第二个.记为a2;……,第n个记为ax,若 a1=![]() ,且从第二个数起,每个数都等于“1与它前面那个数的差的倒数”
,且从第二个数起,每个数都等于“1与它前面那个数的差的倒数”
(1)则a2=______;a3 =______;a4 =______.
(2)根据(1)的计算结果,猜想a2005=______;a2006=______.
(3)计算: ![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店5月1日举行促销优惠活动,当天到该商店购买商品有两种方案,方案一:用168元购买会员卡成为会员后,凭会员卡购买商店内任何商品,一律按商品价格的8折优惠;方案二:若不购买会员卡,则购买商店内任何商品一律按商品价格的9.5折优惠.
(1)若小敏不购买会员卡,所购买商品的价格为120元时,实际应支付多少元?
(2)请帮小敏算一算,她购买商品的价格为多少元时,两个方案所付金额相同?
(3)购买商品的价格______元时,采用方案一更合算.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小红家分了一套住房,她想在自己的房间的墙上钉一根细木条,挂上自己喜欢的装饰物,那么小红至少需要几根钉子使细木条固定( )
A.1根
B.2根
C.3根
D.4根
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去….若点A( ![]() ,0),B(0,2),则点B2016的坐标为 .
,0),B(0,2),则点B2016的坐标为 . 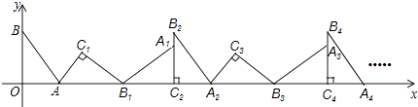
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F. 
(1)求证:OE=OF;
(2)若CE=8,CF=6,求OC的长;
(3)当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com