
分析 (1)原式括号中变形计算后,约分即可得到结果;
(2)根据题意列出算式,计算即可得到结果.
解答 解:(1)原式=-(1-$\frac{1}{2}$)(1-$\frac{1}{3}$)(1-$\frac{1}{4}$)…(1-$\frac{1}{100}$)=-$\frac{1}{2}$×$\frac{2}{3}$×$\frac{3}{4}$×…×$\frac{99}{100}$=-$\frac{1}{100}$;
(2)根据题意得:2006×(1-$\frac{1}{2}$)×(1-$\frac{1}{3}$)×…×(1-$\frac{1}{2006}$)=2006×$\frac{1}{2}$×$\frac{2}{3}$×$\frac{3}{4}$×…×$\frac{2005}{2006}$=1.
点评 此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.


科目:初中数学 来源: 题型:解答题
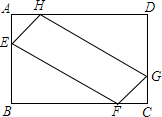 如图,在矩形ABCD中,AB=6,BC=8,点E、F、G、H分别在边AB、BC、CD、AD上,且AE=AH=CF=CG,设AE的长为x,四边形EFGH的面积为S.
如图,在矩形ABCD中,AB=6,BC=8,点E、F、G、H分别在边AB、BC、CD、AD上,且AE=AH=CF=CG,设AE的长为x,四边形EFGH的面积为S.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 若a-b=0,则a=b | B. | 若-$\frac{1}{2}$x=-4,则x=2 | ||
| C. | 若a=b,则2a-5=2b-5 | D. | 若a=b,则$\frac{a}{-4}$=$\frac{b}{-4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 由2x-2y-1得-1-2y+2x | B. | 由6x-1=x+5得6x-1=5+x | ||
| C. | 由4-x=3x-2得3x-2=4-x | D. | 由2-x=x-2得2+2=x+x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com