
����Ŀ����ͼA������������Ӧ����Ϊ��2��
![]()
��1����B�ڵ�A�ұ߾�A��4����λ���ȣ����B����Ӧ������
��2���ڣ�1���������£���A��ÿ��2����λ���������������˶�����B��ÿ��2����λ���������������˶�������A�˶�����6���ڵĵ㴦ʱ����A��B�������룮
��3���ڣ�2���������£���A�㾲ֹ������B�������������˶�ʱ�������ʱ��A��B�������4����λ���ȣ�
���𰸡���1��B����Ӧ����Ϊ2����2��A��B����������12����λ���ȣ���3������4���8�볤ʱ��A��B�������4����λ���ȣ�
��������
��1����������Ҽӿ����B����Ӧ������
��2���ȸ���ʱ�䣽·�̡��ٶȣ�����˶�ʱ�䣬�ٸ���·�̣��ٶȡ�ʱ����⼴�ɣ�
��3��������������˶����B����A���ұ�4����λ���ȣ��˶����B����A�����4����λ���ȣ��г�������⼴�ɣ�
�⣺��1����2+4��2��
�ʵ�B����Ӧ����Ϊ2��
��2������2+6����2��2���룩��
4+��2+2����2��12������λ���ȣ���
��A��B����������12����λ���ȣ�
��3���˶����B����A���ұ�4����λ���ȣ�
�辭��x�볤ʱ��A��B�������4����λ���ȣ���������
2x��12��4��
���x��4��
�˶����B����A�����4����λ���ȣ�
�辭��x�볤ʱ��A��B�������4����λ���ȣ���������
2x��12+4��
���x��8��
�ʾ���4���8�볤ʱ��A��B�������4����λ���ȣ�


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��˾��ij�������Ͷ�Ź�������������ʹ�ã�Ͷ�����ķֲ���Ͷ�ź��ʹ�����ͳ�����£�
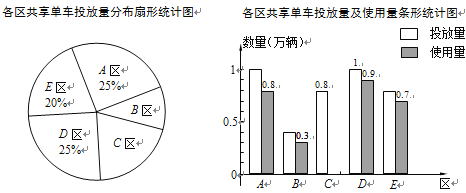
��1���ù�˾��ȫ��һ��Ͷ���� ��������������
��2��������ͳ��ͼ�У�B������Ӧ���ε�Բ�Ľ�Ϊ �㣻
��3���ù�˾��ȫ��Ͷ�ŵĹ���������ʹ����ռͶ������85%�������C������������ʹ��������ȫ����ͳ��ͼ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���۲��±���
��� | 1 | 2 | 3 | ���� |
x x x x | ||||
x x x | y y y | |||
x x | y y | x x x x | ||
ͼ�� | y | x x x | y y y | |
x x | y y | x x x x | ||
x x x | y y y | |||
x x x x |
���ǰ�ij������ĸ�����õ��Ķ���ʽ��Ϊ������ʽ����ʽ���������1��ġ�����ʽ����ʽ��Ϊ4x��y��
��1����3��ġ�����ʽ����ʽ��Ϊ________________��
��2����4��ġ�����ʽ����ʽ��Ϊ________________��
��3����n��ġ�����ʽ����ʽ��Ϊ________________��
��4������1��� ������ʽ����ʽ��Ϊ10����2��ġ�����ʽ����ʽ��Ϊ19����x��y��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ı���ABCD�У��Խ���AC��BD�ཻ�ڵ�O����������������������AB��CD��AD��BC����AB=CD��AD=BC����AO=CO��BO=DO����AB��CD��AD=BC������һ�����ж�����ı�����ƽ���ı��ε���������
A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�������ϰ�Ҫ��ͼ�Σ����ش����⣺
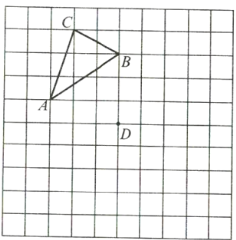
��1�������������![]() ƽ�ƣ�ʹ�õ�
ƽ�ƣ�ʹ�õ�![]() ƽ�Ƶ�ͼ�е�
ƽ�Ƶ�ͼ�е�![]() λ�ã���
λ�ã���![]() ����
����![]() �Ķ�Ӧ��ֱ�Ϊ��
�Ķ�Ӧ��ֱ�Ϊ��![]() ����
����![]() ���뻭��������
���뻭��������![]() ��
��
��2������������![]() ���ڵ�
���ڵ�![]() �����ĶԳƵ�������
�����ĶԳƵ�������![]() ��
��
��3��������![]() ��������
��������![]() ______����ǡ�������ij��������ĶԳƣ�����ǣ�����ͼ�л�������Գ����ģ���������
______����ǡ�������ij��������ĶԳƣ�����ǣ�����ͼ�л�������Գ����ģ���������![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ -3��-1��0��1��3��������������ȡһ������Ϊa���ٴ�ʣ�µ��ĸ����������ȡһ������Ϊb��ǡ��ʹ����x��y�Ķ�Ԫһ�η�����![]() �������⣬�ҵ�(a��b)����˫����
�������⣬�ҵ�(a��b)����˫����![]() �ϵĸ�����_________.
�ϵĸ�����_________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������װƷ����Ƴ���һ����װ���������װÿ����200Ԫ�����ÿ������40Ԫ�����ƹ��װƷ�Ƴ��ڿ�չ�����������ͬʱ��ͻ��ṩ�����Żݷ�����
��������һ����װ��һ�������
��������װ������������۵�90%���
��ij�ͻ�Ҫ���÷�װƷ�ƹ�����װ20�ף����![]() ����
����![]() ����20����
����20����
��1�����ÿͻ��������������踶��_ _____Ԫ���ú�![]() ��ʽ�ӱ�ʾ����
��ʽ�ӱ�ʾ����
���ÿͻ��������������踶��__ ____Ԫ���ú�![]() ��ʽ�ӱ�ʾ����
��ʽ�ӱ�ʾ����
��2����![]() =30��ͨ������˵����ʱ�����ַ��������Ϊ���㣿
=30��ͨ������˵����ʱ�����ַ��������Ϊ���㣿
��3����![]() =30ʱ�����ܸ���һ�ָ�ΪʡǮ�Ĺ�������д����Ĺ�����������������Ǯ����
=30ʱ�����ܸ���һ�ָ�ΪʡǮ�Ĺ�������д����Ĺ�����������������Ǯ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
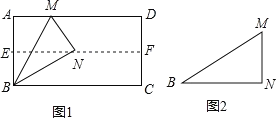
����Ŀ��ʵ��̽����
(1)��ͼ1�����۾���ֽƬABCD��ʹAD��BC�غϣ��õ��ۺ�EF����ֽƬչ������һ���۵�ֽƬ��ʹ��A����EF�ϣ���ʹ�ۺ۾�����B���õ��ۺ�BM��ͬʱ�õ��߶�BN��MN.����۲�ͼ1�������MBN�Ķ����Ƕ��٣���֤����Ľ���.
(2)��ͼ1�е�������ֽƬBMN���£���ͼ2���۵���ֽƬ��̽��MN��BM��������ϵ��д���۵�����������Ϸ���֤����Ľ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ������⣺
�������ʽ�ֽ���һ�ּ��ɽ�ǿ�ķ�������ͨ���ǰѶ���ʽ�е�ijһ���ɼ���ٷ���ֽ⣬�����ʱ��Ҫ���ʵ����ܳɹ��������![]() �ֽ���ʽ������һ������ʽ����ߴ����������һ����ϵ��Ϊ�㣬�����û�й���ʽ����ȡ���ֲ���ֱ��Ӧ�ù�ʽ����������������ֽ���������ѳ�������1��3��ԭʽ�ͱ��
�ֽ���ʽ������һ������ʽ����ߴ����������һ����ϵ��Ϊ�㣬�����û�й���ʽ����ȡ���ֲ���ֱ��Ӧ�ù�ʽ����������������ֽ���������ѳ�������1��3��ԭʽ�ͱ��![]() ����������������ƽ�����ȷֽ⣬�ⷨ���£�
����������������ƽ�����ȷֽ⣬�ⷨ���£�
ԭʽ![]()
![]()
��ʽ��![]() ��
��![]()
���������۷��ͽⷨ��
��1����ʽ�ֽ⣺![]() ��
��
��2����ʽ�ֽ⣺![]() ��
��
��3����ʽ�ֽ⣺![]() ��
��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com