
| A、9 | ||
| B、8 | ||
| C、1 | ||
D、
|
|
| 4 |
| 3 |
| 4 |
| 3 |
| 2 |
| 2×1 |


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
| A、1个 | B、2个 | C、3个 | D、4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,杭州市郊外一景区内有一条笔直的公路a经过两个景点A,B,景区管委会又开发了风景优美的景点C,经测量景点C位于景点A的北偏东60°方向,又位于景点B的北偏东30°方向,且景点A、B相距200m,则景点B、C相距的路程为( )
如图,杭州市郊外一景区内有一条笔直的公路a经过两个景点A,B,景区管委会又开发了风景优美的景点C,经测量景点C位于景点A的北偏东60°方向,又位于景点B的北偏东30°方向,且景点A、B相距200m,则景点B、C相距的路程为( )A、100
| ||
| B、200 | ||
| C、100 | ||
D、200
|
查看答案和解析>>
科目:初中数学 来源: 题型:
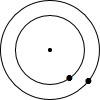 如图,有2个同心圆,半径分别为R和r(单位:厘米),且R>r>1,记两圆之间的圆环面积为P;若把R和r都增加1厘米,记两圆之间的圆环面积为Q,则( )
如图,有2个同心圆,半径分别为R和r(单位:厘米),且R>r>1,记两圆之间的圆环面积为P;若把R和r都增加1厘米,记两圆之间的圆环面积为Q,则( )A、0<
| ||
B、1<
| ||
C、2<
| ||
D、3<
|
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、5 | B、6 | C、7 | D、8 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| a |
| 4 |
| A、①④ | B、②④ | C、①②④ | D、①③ |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,直线y=-x+3与x轴交于点A,与y轴交于点B,抛物线y=-x2+bx+c经过点A、B.
如图,直线y=-x+3与x轴交于点A,与y轴交于点B,抛物线y=-x2+bx+c经过点A、B.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com