
【题目】如图,在矩形![]() 中,点
中,点![]() 是
是![]() 的中点,将
的中点,将![]() 沿
沿![]() 折叠后得到
折叠后得到![]() ,且点
,且点![]() 在矩形
在矩形![]() 的内部,将
的内部,将![]() 延长交
延长交![]() 于点
于点![]() ,若
,若![]() ,则
,则![]() ______.
______.
【答案】![]()
【解析】
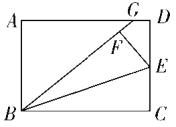
根据中点定义可得DE=CE,再根据翻折的性质可得CE=EF,BF=BC,∠BFE=∠C=90°,从而得到DE=EF,连接EG,利用“HL”证明Rt△EFG和Rt△EDG全等,根据全等三角形对应边相等可得DG=FG,设DG=a,表示出AG,然后求出AD,再根据矩形的对边相等可得AD=BC,从而求出BF,再求出BG,然后利用勾股定理列式求出AB,再求比值即可.
解:连接EG, ∵点E是边CD的中点,
∴DE=CE,
∵将△BCE沿BE折叠后得到△BFE,
∴CE=EF,BC=BF,∠BFE=∠C=90°,
∴DE=EF, ![]()
在Rt△EDG和Rt△EFG中,
![]() ,
,
∴Rt△EFG≌Rt△EDG(HL),
∴DG=FG,
设DG=a,
∵![]() ,
,
∴GA=4a,
∴AD=AG+DG=a+4a=5a,
在矩形ABCD中,AD=BC=5a,
∴BF=5a, BG=BF+FG=5a+a=6a,
在Rt△ABG中,AB=![]()
∴ ![]()

故答案为:![]()


 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】下面是小明设计的“在已知三角形的一边上取一点,使得这点到这个三角形的另外两边的距离相等”的尺规作图过程:
已知:△ABC.
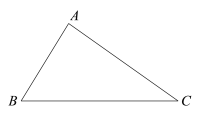
求作:点D,使得点D在BC边上,且到AB,AC边的距离相等.
作法:如图,
作∠BAC的平分线,交BC于点D.则点D即为所求.
根据小明设计的尺规作图过程,
(1)使用直尺和圆规,补全图形 (保留作图痕迹);
(2)完成下面的证明.
证明:作DE⊥AB于点E,作DF⊥AC于点F,
∵AD平分∠BAC,
∴ = ( ) (填推理的依据) .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,函数
中,函数![]() (
(![]() )的图象G与直线
)的图象G与直线![]() 交于点A(4,1),点B(1,n)(n≥4,n为整数)在直线l上.
交于点A(4,1),点B(1,n)(n≥4,n为整数)在直线l上.
(1)求![]() 的值;
的值;
(2)横、纵坐标都是整数的点叫做整点.记图象![]() 与直线l围成的区域(不含边界)为W.
与直线l围成的区域(不含边界)为W.
①当n=5时,求![]() 的值,并写出区域W内的整点个数;
的值,并写出区域W内的整点个数;
②若区域W内恰有5个整点,结合函数图象,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)“六·一”儿童节前,某玩具商店根据市场调查,用2500元购进一批儿童玩
具,上市后很快脱销,接着又用4500元购进第二批这种玩具,所购数量是第一批数量的1.5
倍,但每套进价多了10元.
(1)求第一批玩具每套的进价是多少元?
(2)如果这两批玩具每套售价相同,且全部售完后总利润不低于25%,那么每套售价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一部记录片播放了关于地震的资料及一个有关地震预测的讨论,一位专家指出:“在未来20年,A城市发生地震的机会是三分之二”
对这位专家的陈述下面有四个推断:
①![]() ×20≈13.3,所以今后的13年至14年间,A城市会发生一次地震;
×20≈13.3,所以今后的13年至14年间,A城市会发生一次地震;
②![]() 大于50%,所以未来20年,A城市一定发生地震;
大于50%,所以未来20年,A城市一定发生地震;
③在未来20年,A城市发生地震的可能性大于不发生地震的可能性;
④不能确定在未来20年,A城市是否会发生地震;
其中合理的是( )
A. ①③ B. ②③ C. ②④ D. ③④
查看答案和解析>>
科目:初中数学 来源: 题型:
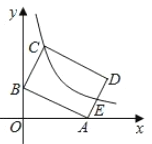
【题目】如图,在平面直角坐标系中,点A(4,0),B(0,2),反比例函数![]() 的图象经过矩形ABCD的顶点C,且交边AD于点E,若E为AD的中点,则k的值为__________.
的图象经过矩形ABCD的顶点C,且交边AD于点E,若E为AD的中点,则k的值为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果商将一种高档水果放在商场销售,该种水果成本价为10元![]() ,售价为40元
,售价为40元![]() ,每天可销售20
,每天可销售20![]() .调查发现,销售单价每下降1元,每天的销售量将增加5
.调查发现,销售单价每下降1元,每天的销售量将增加5![]() .
.
(1)直接写出每天的销售量ykg与降价![]() (元)之间的函数关系式;
(元)之间的函数关系式;
(2)降价多少元时,每天的销售额![]() 元最大,最大是多少元?(销售额=售价×数量)
元最大,最大是多少元?(销售额=售价×数量)
(3)每销售1![]() 水果,需向商场缴纳柜台费
水果,需向商场缴纳柜台费![]() 元(
元(![]() ),水果商计划租赁柜台20天,为了促销,决定开展“每天降价1元”活动,即从第1天开始,每天的销售单价比前一天下降1元(第1天的销售单价为39元),经测算发现,销售的前11天,每天的利润
),水果商计划租赁柜台20天,为了促销,决定开展“每天降价1元”活动,即从第1天开始,每天的销售单价比前一天下降1元(第1天的销售单价为39元),经测算发现,销售的前11天,每天的利润![]() 元随销售天数
元随销售天数![]() (
(![]() 为正整数)的增大而增大,试确定
为正整数)的增大而增大,试确定![]() 的取值范围.(利润=销售额-成本-柜台费)
的取值范围.(利润=销售额-成本-柜台费)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com