
 下面的判断是否正确.说明理由:
下面的判断是否正确.说明理由:分析 利用反例对(1)、(3)进行判断;根据0到9的平方的末位数都不是2可对(2)进行判断;根据三角形面积公式对(4)进行判断;根据正方形的性质对(5)进行判断.
解答 解:当a=1,b=-1时,a+b≠a-b,所以(1)错误;
任何一个整数的平方,末位数都不是2,所以(2)正确;
如果a>b,若a=0,b=-1,则a-5=b-4,所以(3)错误;
两个角形的底边不等.高也不等,而它们的积相等,则两个三角形的面积相等,所以(4)错误;
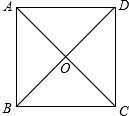
如图,如果ABCD是正方形,那么连接AC,BD后,正方形被分成的四个等腰直角三角形,这些三角形全等,所以(5)正确.
点评 本题考查了命题与定理:判断一件事情的语句,叫做命题.许多命题都是由题设和结论两部分组成,题设是已知事项,结论是由已知事项推出的事项,一个命题可以写成“如果…那么…”形式. 有些命题的正确性是用推理证实的,这样的真命题叫做定理.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
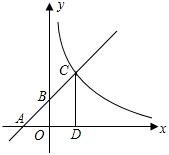 如图,已知一次函数y=kx+b的图象与x轴,y轴分别相交于A,B两点,且与反此列函数y=$\frac{m}{x}$在第一象限的图象交于点C,CD垂直于x轴,垂足为D.如果OA=OB=OD=1,求:
如图,已知一次函数y=kx+b的图象与x轴,y轴分别相交于A,B两点,且与反此列函数y=$\frac{m}{x}$在第一象限的图象交于点C,CD垂直于x轴,垂足为D.如果OA=OB=OD=1,求:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
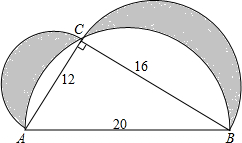 有一个著名的希波克拉蒂月牙问题,如图,以AB为直径作半圆,C是圆弧上一点(不与A、B重合),以AC、BC为直径分别作半圆,围成两个月牙(阴影部分).已知直径AB=20cm,直径AC=12cm,直径BC=16cm.(注:此时∠ACB是直角)
有一个著名的希波克拉蒂月牙问题,如图,以AB为直径作半圆,C是圆弧上一点(不与A、B重合),以AC、BC为直径分别作半圆,围成两个月牙(阴影部分).已知直径AB=20cm,直径AC=12cm,直径BC=16cm.(注:此时∠ACB是直角)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图,在数轴上,点A表示的数为10,点B表示的数为13,点M丧示的数是-20.求:
已知:如图,在数轴上,点A表示的数为10,点B表示的数为13,点M丧示的数是-20.求:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
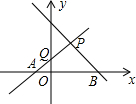 如图,直线PA是一次函数y=x+n(n>0)的图象,直线PB是一次函数y=-2x+m(m>0)的图象.
如图,直线PA是一次函数y=x+n(n>0)的图象,直线PB是一次函数y=-2x+m(m>0)的图象.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com