
分析 (1)将甲乙两地的路程看作单位1,可得到辆车的速度,然后依据路程=时间×速度列方程求解即可;
(2)依据快车行驶的路程+慢车形行驶等于总路程列方程求解即可.
解答 解:(1)设两车同时开出x小时后相遇.
根据题意得:$\frac{1}{6}$x+$\frac{1}{10}$x=1.
解得:x=$\frac{15}{4}$.
答:辆车同时开出$\frac{15}{4}$小时后相遇.
(2)慢车开出y小时后两车相遇.
根据题意得:(2+y)×$\frac{1}{6}$+$\frac{1}{10}$y=1.
解得:y=2.5.
慢车开出2.5小时后辆车相遇.
点评 本题主要考查的是一元一次方程的应用,将甲乙两地之间的距离看作单位1是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
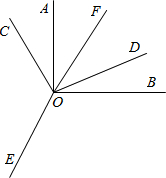 如图,平面内∠AOB=∠COD=90°,∠COE=∠BOE,OF平分∠AOD.则以下结论:
如图,平面内∠AOB=∠COD=90°,∠COE=∠BOE,OF平分∠AOD.则以下结论:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-7)×$\frac{4}{3}$×(-2.5) | B. | (-7)×(-$\frac{4}{3}$)×(-2.5) | C. | (-7)×(-$\frac{4}{3}$)×(-$\frac{2}{5}$) | D. | (-7)×(-$\frac{3}{4}$)×(-$\frac{5}{2}$) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
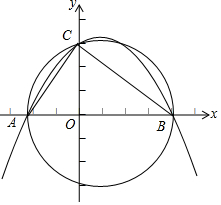 如图已知A(-$\frac{9}{4}$,0),C(0,3),B为x轴中正半轴上的点,以AB为直径的圆过C点.
如图已知A(-$\frac{9}{4}$,0),C(0,3),B为x轴中正半轴上的点,以AB为直径的圆过C点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 0 | 1 | 2 | 3 | … |
| 1 | 3 | 5 | 7 | … |
| 2 | 5 | 8 | 11 | … |
| 3 | 7 | 11 | 15 | … |
| 4 | 9 | … | … | … |
| 9 |
| 14 |
| a |
| 11 | 13 |
| 17 | b |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com