
 如图,△ABC内接于⊙O,OD⊥BC于D,∠OCD=40°,则弦BC所对圆周角的度数是( )
如图,△ABC内接于⊙O,OD⊥BC于D,∠OCD=40°,则弦BC所对圆周角的度数是( )| A、40° |
| B、50° |
| C、50°或130° |
| D、40°或140° |
| 1 |
| 2 |
 |
| BC |
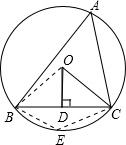 解:连接OB,
解:连接OB,| 1 |
| 2 |
 |
| BC |


科目:初中数学 来源: 题型:
| A、度量三角形的内角和,结果是360° |
| B、从装有5个黑球的口袋中摸出一球是黑球 |
| C、实数a的平方为负数 |
| D、购买100张中奖率为1%的彩票,结果中奖 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,直线AB过x轴上一点A(2,0),且与抛物线y=ax2相交于B、C两点,B点坐标为(1,1).
如图,直线AB过x轴上一点A(2,0),且与抛物线y=ax2相交于B、C两点,B点坐标为(1,1).查看答案和解析>>
科目:初中数学 来源: 题型:
| A、p=12,m=14 |
| B、p=-12,m=15 |
| C、p=-12,m=-9 |
| D、p=12,m=9 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com