
【题目】如图,AB为⊙O直径,C、D为⊙O上不同于A、B的两点,∠ABD=2∠BAC.过点C作CE⊥DB,垂足为E,直线AB与CE相交于F点.
(1)求证:CF为⊙O的切线;
(2)若CE=2,BE=1,求BD长.
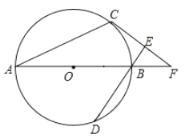
【答案】(1)见解析;(2)BD=3
【解析】
(1)连结OC,由于∠A=∠OCA,则根据三角形外角性质得∠BOC=2∠A,而∠ABD=2∠BAC,所以∠ABD=∠BOC,根据平行线的判定得到OC∥BD,再CE⊥BD得到OC⊥CE,然后根据切线的判定定理得CF为⊙O的切线;
(2)过点O作OG⊥DE,垂足为G,则可证四边形OCEG是矩形,可得OG=CE=2,OC=GE=1+GB,根据勾股定理可求GB的长,根据垂径定理可求BD的长.
解:(1)如图:连结OC,
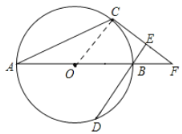
∵OA=OC,
∴∠A=∠OCA,
∴∠BOC=∠A+∠OCA=2∠A,
∵∠ABD=2∠BAC,
∴∠ABD=∠BOC,
∴OC∥BD,
∵CE⊥BD,
∴OC⊥CE,
∴CF为⊙O的切线;
(2)如图:过点O作OG⊥DE,垂足为G
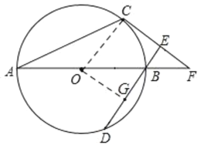
∵OG⊥DE,OC⊥CE,DE⊥CE
∴四边形OCEG是矩形
∴OG=CE=2,OC=GE=1+GB
在Rt△OGB中,OB2=OG2+GB2.
∴(1+GB)2=4+GB2.
∴GB=![]() ,
,
∵OG⊥DB
∴BD=2GB=3


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
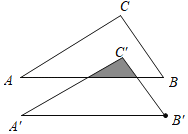
【题目】如图,将Rt△ABC平移到△A'B'C'的位置,其中∠C=90°使得点C'与△ABC的内心重合,已知AC=4,BC=3,则阴影部分的面积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
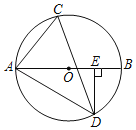
【题目】如图,AB是⊙O的直径,D是⊙O上一点,DE⊥AB于点E,且∠ADE=60°,C是![]() 上一点,连结AC,CD.
上一点,连结AC,CD.
(1)求∠ACD的度数;
(2)证明:AD2=ABAE;
(3)如果AB=8,∠ADC=45°,请你编制一个计算题(不标注新的字母),并直接给出答案.(根据编出的问题层次,给不同的得分)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2017重庆A卷第11题)如图,小王在长江边某瞭望台D处,测得江面上的渔船A的俯角为40°,若DE=3米,CE=2米,CE平行于江面AB,迎水坡BC的坡度i=1:0.75,坡长BC=10米,则此时AB的长约为( )(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84).

A. 5.1米 B. 6.3米 C. 7.1米 D. 9.2米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究
问题情境:
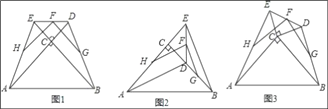
(1)如图1,两块等腰直角三角板△ABC和△ECD如图所示摆放,其中∠ACB=∠DCE=90°,点F,H,G分别是线段DE,AE,BD的中点,A,C,D和B,C,E分别共线,则FH和FG的数量关系是 ,位置关系是 .
合作探究:
(2)如图2,若将图1中的△DEC绕着点C顺时针旋转至A,C,E在一条直线上,其余条件不变,那么(1)中的结论还成立吗?若成立,请证明,若不成立,请说明理由.
(3)如图3,若将图1中的△DEC绕着点C顺时针旋转一个锐角,那么(1)中的结论是否还成立?若成立,请证明,若不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(-4, 1),B(-1,3),C(-1,1)
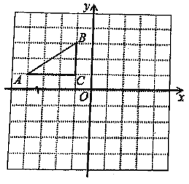
(1)将△ABC以原点O为旋转中心旋转180°,画出旋转后对应的△![]() ;平移△ABC,若A对应的点
;平移△ABC,若A对应的点![]() 坐标为(-4,-5),画出△
坐标为(-4,-5),画出△![]() ;
;
(2)若△![]() 绕某一点旋转可以得到△
绕某一点旋转可以得到△![]() ,直接写出旋转中心坐标是__________;
,直接写出旋转中心坐标是__________;
(3)在x轴上有一点P是的PA+PB的值最小,直接写出点P的坐标___________;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() ,
,![]() 与
与![]() 的部分对应值如下表所示:
的部分对应值如下表所示:
| … | -1 | 0 | 1 | 2 | 3 | 4 | … |
| … | 6 | 1 | -2 | -3 | -2 | m | … |
下面有四个论断:
①抛物线![]() 的顶点为
的顶点为![]() ;
;
②![]() ;
;
③关于![]() 的方程
的方程![]() 的解为
的解为![]() ;
;
④![]() .
.
其中,正确的有___________________
查看答案和解析>>
科目:初中数学 来源: 题型:
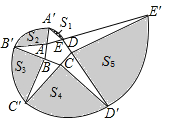
【题目】如图以正五边形ABCDE的顶点A为圆心,AE为半径作圆弧交BA的延长线于点A′,再以点B为圆心,BA′为半径作圆弧交CB的延长线于B′,依次进行.得到螺旋线,再顺次连结EA′,AB′,BC′,CD′,DE′,得到5块阴影区域,若记它们的面积分别为S1,S2,S3,S4,S5,且满足S5﹣S2=1,则S4﹣S3的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com