
【题目】如图,将Rt△ABC平移到△A'B'C'的位置,其中∠C=90°使得点C'与△ABC的内心重合,已知AC=4,BC=3,则阴影部分的面积为( )
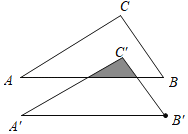
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
由三角形面积公式可求C'E的长,由相似三角形的性质可求解.
如图,过点C'作C'E⊥AB,C'G⊥AC,C'H⊥BC,并延长C'E交A'B'于点F,连接AC',BC',CC',
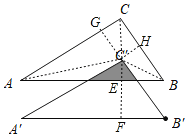
∵点C'与△ABC的内心重合,C'E⊥AB,C'G⊥AC,C'H⊥BC,
∴C'E=C'G'=C'H,
∵S△ABC=S△AC'C+S△AC'B+S△BC'C,
∴![]() AC×BC=
AC×BC=![]() AC×CC'+
AC×CC'+![]() BA×C'E+
BA×C'E+![]() BC×C'H
BC×C'H
∴C'E=1,
∵将Rt△ABC平移到△A'B'C'的位置,
∴AB∥A'B',AB=A'B',A'C'=AC=4,B'C'=BC=3
∴C'F⊥A'B',A'B'=5
∴![]() A'C'×B'C'=
A'C'×B'C'=![]() A'B'×C'F
A'B'×C'F
∴C'F=![]()
∵AB∥A'B'
∴△C'MN∽△C'A'B',
∴S阴影部分=S△C'A'B'×(![]() )2,
)2,
∴S阴影部分=![]() ×4×3×
×4×3×![]() =
=![]()
故选:D.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
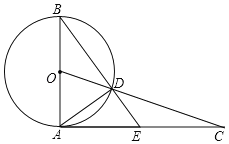
【题目】如图,AB是⊙O的直径,过点A作⊙O的切线并在其上取一点C,连接OC交⊙O于点D,BD的延长线交AC于E,连接AD,
(1)求证:CD2=CEAC;
(2)若AB=4,AC=4![]() ,求AE的长.
,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+3经过A(3,0),B(1,0)两点(如图1),顶点为M.
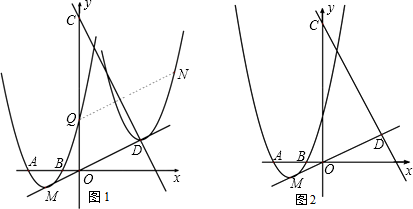
(1)a、b的值;
(2)设抛物线与y轴的交点为Q(如图1),直线y=2x+9与直线OM交于点D. 现将抛物线平移,保持顶点在直线OD上.当抛物线的顶点平移到D点时,Q点移至N点,求抛物线上的两点M、Q间所夹的曲线MQ扫过的区域的面积;
(3)设直线y=2x+9与y轴交于点C,与直线OM交于点D(如图2).现将抛物线平移,保持顶点在直线OD上.若平移的抛物线与射线CD(含端点C)没有公共点时,试探求其顶点的横坐标h的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点C在线段AB上,(点C不与A、B重合),分别以AC、BC为边在AB同侧作等边三角形ACD和等边三角形BCE,连接AE、BD交于点P.
(观察猜想)
①AE与BD的数量关系是 ;
②∠APD的度数为 .
(数学思考)
如图2,当点C在线段AB外时,(1)中的结论①、②是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明;
(拓展应用)
如图3,点E为四边形ABCD内一点,且满足∠AED=∠BEC=90°,AE=DE,BE=CE,对角线AC、BD交于点P,AC=10,则四边形ABCD的面积为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
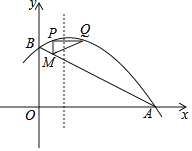
【题目】如图,在平面直角坐标系中,抛物线y=ax2+![]() x+2与x轴交于点A(4,0)与y轴交于点B.点M在线段AB上,其横坐标为m,PM∥y轴,与抛物线交点为点P,PQ∥x轴,与抛物线交点为点Q
x+2与x轴交于点A(4,0)与y轴交于点B.点M在线段AB上,其横坐标为m,PM∥y轴,与抛物线交点为点P,PQ∥x轴,与抛物线交点为点Q
(1)求a的值、并写出此抛物线顶点的坐标;
(2)求m为何值时,△PMQ为等腰直角三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
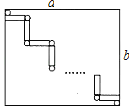
【题目】如图由长为a,宽为b的矩形、(2m+1)个长为4,宽为1的小矩形(为正整数)和若干个小圆组成,其中小圆的直径与小矩形的宽相等.
(1)当m=1时,a= ,b= ;
(2)当a=24时,求b的值;
(3)a的值能否等于30?请通过计算说明理由;
(4)直接写出a与b的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程![]() 有两个实数根x1,x2.
有两个实数根x1,x2.
(1)求实数k的取值范围;
(2)是否存在实数k使得![]() 成立?若存在,请求出k的值;若不存在,请说明理由.
成立?若存在,请求出k的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
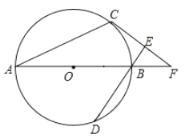
【题目】如图,AB为⊙O直径,C、D为⊙O上不同于A、B的两点,∠ABD=2∠BAC.过点C作CE⊥DB,垂足为E,直线AB与CE相交于F点.
(1)求证:CF为⊙O的切线;
(2)若CE=2,BE=1,求BD长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com